알고리즘이란
알고리즘이란 어떠한 문제를 해결하기 위한 여러 동작들의 모임을 말한다. 알고리즘은 유한성을 가지며, 언젠가는 끝나야하는 속성을 가지고 있다.
좋은 알고리즘을 작성하기 위해서는 항상 효율성을 고려해야 한다.
이때, 알고리즘의 복잡도를 판단하는 척도로 공간복잡도와 시간복잡도를 계산하게 된다. 그 중 시간 복잡도는 알고리즘 내 연산의 횟수와 밀접한 관계가 있다.
시간 복잡도
시간 복잡도는 알고리즘의 수행시간을 말한다.
공간 복잡도
공간 복잡도는 알고리즘 실행에 필요한 메모리의 양을 말한다.
사실 위 2가지 복잡도 중 좀 더 주안점을 두고 보는 것은 시간복잡도인데, 공간에 대한 부분은 하드웨어의 발달로 인해 상대적으로 비중이 줄었기 때문이다.
또한 시간복잡도와 공간복잡도는 일반적으로 반비례하는 성질을 가진다.
시간 복잡도 표기법
빅오 표기법(Big-O)는 시간 복잡도를 나타내는 표기법 중 가장 많이 사용되는 표기법이다.
알고리즘의 최악의 실행 시간을 표기하며, 최소한 보장되는 성능을 표기하기 때문에 가장 일반적으로 사용한다.
이러한 빅오 표기법의 특징은 시간복잡에 미미한 영향을 주는 것들은 배제하고 표기되는 특징을 가지며 정리해보면 다음과 같다.
- 상수항을 무시: O(N+5) -> O(N)
- 계수도 무시: O(3N) -> O(N)
- 최고차항만 표기: O(3N^3+2N^2+N+5) -> O(N^3)
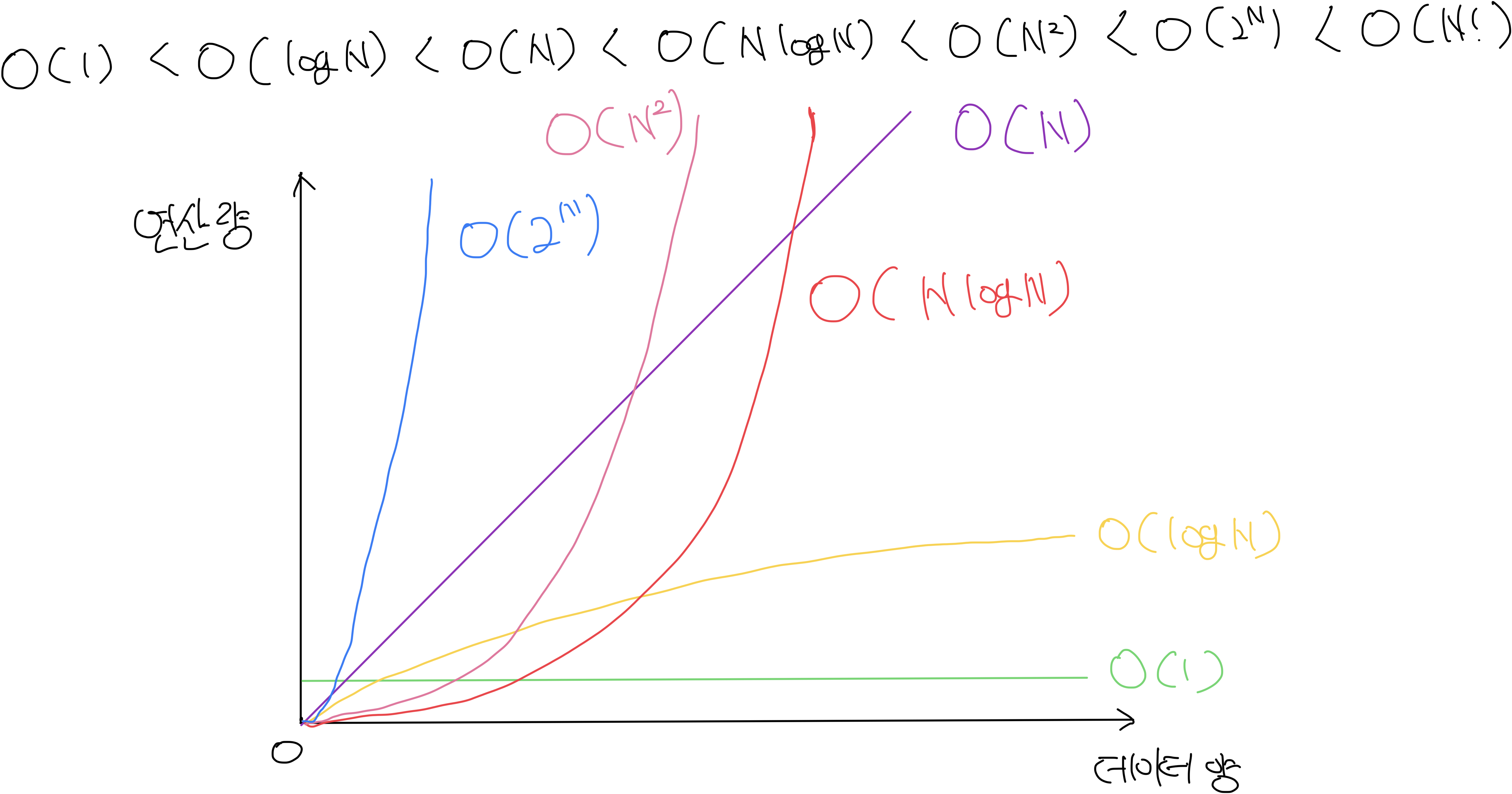
빅오 표기법의 성능 순서는 다음과 같이 나타낼 수 있다.
가장 왼쪽 O(1)으로 갈수록 실행 횟수가 적고, 시간 복잡도가 낮은 것이라고 말할 수 있고, 가장 오른쪽 O(n!)으로 갈수록 실행 횟수가 많고, 시간 복잡도가 높은 것이라고 말할 수 있다.
- O(1)
- 입력값 N이 증가하더라도 실행시간은 동일한 알고리즘
- 인덱스로 접근하여 바로 처리할 수 있는 연산 과정의 시간 복잡도
- stack의 push, pop
- O(logN)
- 연산이 한번 실행될 때마다 데이터의 크기가 절반 감소하는 알고리즘
- binary search 알고리즘, tree 형태 자료구조 탐색
- O(N)
- 입력값이 증가함에 따라 실행시간도 선형적으로 증가하는 알고리즘
- 1중 for문
- O(NlogN)
- O(N)의 알고리즘과 O(logN)의 알고리즘이 중첩된 형태
- 퀵/ 병합/ 힙 정렬
- O(N^2)
- O(N)의 알고리즘이 2번 중첩된 형태
- 2중 for문, 삽입/버블/선택 정렬
- O(2^N)
- 빅오 표기법 중 가장 느린 시간 복잡도로 주로 재귀적으로 수행하는 알고리즘이 이에 해당한다.
- *피보나치 수열
참고로,
빅오메가(Big-Ω) 표기법은 알고리즘 최상의 실행 시간을 표기한다.
빅세터(Big-θ) 표기법은 알고리즘 평균 실행 시간을 표기한다.
피보나치 수열(Fibonacci Sequence)이란?
피보나치 수열은 첫 번째 항과 두 번째 항이 1이며 그 뒤의 항은 바로 앞 두 항의 합인 수열이다. 이 수열의 항을 피보나치 수(Fibonacci Number)라고 부른다. 편의상 0을 0번째 항으로 놓기도 한다.
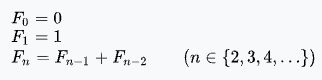
인용
[알고리즘] 빅오 표기법(big-O notation)이란?
알고리즘의 복잡도를 판단하는 척도는 시간 복잡도와 공간 복잡도가 있다. 그 중 시간 복잡도는 알고리즘 내 연산의 횟수와 밀접한 관계가 있다. Big-O(빅 오) 표기법 알고리즘 최악의 실행 시간
velog.io
[Algorithm] 시간 복잡도 / 빅오 표기법
시간 복잡도 > 시간 복잡도(Time Complexity)는 알고리즘의 실행 속도를 말한다 알고리즘은 하나의 문제를 풀 때 여러가지의 코드를 사용하여 풀 수 있다. 문제 풀이에 대한 방법은 여러가지가 있겠
velog.io
'컴퓨터 사이언스 > 개발 상식' 카테고리의 다른 글
| 반복문, 재귀함수 (0) | 2023.10.16 |
|---|---|
| html - div, article, section 의 차이 (0) | 2023.08.12 |
| API remind (0) | 2023.08.10 |
| 크롬 개발자도구 이용한 디버깅 (0) | 2023.05.07 |
| API에 관하여 (0) | 2023.05.06 |
