C 프로그래머들은 대개 추가적인 가상메모리를 런타임에 획득할 필요가 있을 때, 동적 메모리 할당기를 사용하는 것을 선호한다. 여기서 동적 메모리 할당기는 heap이라고 하는 프로세스의 가상메모리 영역을 관리한다. 물론 자세한 내용은 시스템마다 다르지만, 힙은 미초기화된 데이터 영역 직후에 시작해서 위쪽으로 커지는 무요구 메모리 영역이라고 가정한다. 이때, 각각의 프로세스에 대해서 커널은 힙의 꼭대기를 가리키는 변수 brk를 사용한다. 그리고 할당기는 힙을 다양한 크기의 블록들의 집합으로 관리하는데, 각 블록은 할당되었거나 가용한 가상메모리의 연속적인 묶음이다.
할당기들은 2가지의 기본 유형이 있고, 두 유형 모두 응용 프로그램이 명시적으로 블록을 할당하도록 요구한다. 다만, 이들은 어떤 엔트리가 할당된 블록을 반환하기 위해서 무엇이 사용되어야 하는지에 대해서 차이가 난다.
그럼 우선 명시적(explicit) 할당기에 대해서 알아보자. 이 할당기는 응용 프로그램이 명시적으로 할당된 블록을 반환해 줄 것을 요구한다. 예를 들어서, C 표준 라이브러리는 malloc 패키지라고 하는 명시적 할당기를 제공하는데, C 프로그램은 malloc 함수를 호출해서 블록을 할당하고, free 함수를 호출해서 블록을 반환한다.
반면에 묵시적(implicit) 할당기는 garbage collector라고 알려져 있으며, 자동으로 사용하지 않은 할당된 블록을 반환시켜주는 작업을 garbage collection이라고 한다.
malloc과 free함수
C 표준 라이브러리는 malloc 패키지로 알려진 explicit 할당기를 제공한다. 프로그램은 malloc 함수를 호출해서 heap으로부터 블록들을 할당받는다. 그리고 malloc 함수는 블록 내에 포함될 수 있는 어떤 종류의 데이터 객체에 대해서 적절히 정렬된 최소 size 바이트를 갖는 메모리 블록의 포인터를 return한다.
#include <stdlib.h>
void *malloc(size_t size);
void free(void *ptr);
void *calloc(size_t nmemb, size_t size);
void *realloc(void *ptr, size_t size);
void *reallocarray(void *ptr, size_t nmemb, size_t size);
그리고 실제로는 코드가 32 bit mode 또는 64 bit mode 어디에서 동작하도록 컴파일되었는지에 따라 다르다. 32 비트 모드에서는 malloc은 주소가 항상 8의 배수인 블록을 반환하고, 64 비트 모드에서 항상 16의 배수인 블록을 반환한다.
또한 만약 프로그램이 가용한 가상메모리보다 더 큰 크기의 메모리 블록을 요청하는 경우에는 null을 반환하고, errno를 설정한다.
malloc과 같은 동적 메모리 할당기는 mmap과 munmap, sbrk 같은 함수를 사용해서 명시적으로 heap 메모리를 할당하거나 반환한다.
#include <unistd.h>
int brk(void *addr);
void *sbrk(intptr_t increment);sbrk 함수는 커널의 brk 포인터에 increment를 더해서 힙을 늘리거나 줄여준다. 그리고 만약 성공하면, 이전 brk 값을 반환하고, 아니면 -1을 반환해서 errno를 ENOMEM으로 설정한다. 또 만야게 increment가 0이면, sbrk는 현재의 brk 값을 반환한다.
프로그램들은 할당된 heap 블록을 free 함수를 호출해서 반환하는데, 이때 ptr 인자는 malloc, calloc, realloc에서 획득한 할당된 블록의 시작을 가리켜야 한다. 그렇지 않다면 free의 동작은 정의되지 않는다. 여기서 심각한 문제는 아무것도 반환하지 않기 때문에 free는 응용 프로그램에게 무언가 잘못되었다는 것을 알릴 수 없다는 것이다.
왜 동적 메모리 할당인가?
그렇다면 왜 동적 메모리 할당을 사용해야 할까? 그 답은 배열은 정해진 크기를 사용해서 할당하기 때문이다. 즉, 고정된 배열 크기로 인해 재컴파일이 필요할 수도 있다는 소리이다. 그래서 n 값을 알 수 있을 때, 배열을 런타임에 동적으로 할당하는 동적 메모리 할당 방법이 필요한 것이다. 이로인해 배열의 최대 크기는 가용한 가상메모리의 양에 의해서만 제한이 된다.
이렇듯 동적 메모리 할당은 유용하고 중요한 프로그래밍 기술이다. 그래서 프로그래머들은 동적 할당기를 정확하고 효율적으로 사용하기 위해서 어떻게 이들이 동작하는지 이해할 필요가 있다.
할당기 요구사항과 목표
명시적 할당기들은 다음과 같이 다소 엄격한 제한사항 내에서 동작해야 한다.
- 응용 프로그램은 임의의 순서대로 할당과 반환 요청을 할 수 있다. 그래서 할당기는 할당과 반환 요청의 순서에 대해서 보장할 수 없다. 즉, 할당과 반환 free 요청이 연속되다는 가정을 할 수 없다는 의미이다.
- 할당기는 어떤 종류의 데이터 객체라도 블록에 저장할 수 있도록 요청에 즉시 응답할 수 있어야 한다.
- 확장성을 갖기 위해서 할당기가 사용하는 비확장성 자료 구조들은 heap 자체에 저장되어야 한다.
- 할당기는 블록들을 이들이 어떤 종류의 데이터 객체라도 저장할 수 있도록하는 방식으로 정렬해야 한다.
- 할당기는 일단 블록이 할당되면 이들을 수정하거나 이동하지 않는다. 그래서 할당된 블록들을 압축하는 것과 같은 기법은 존재하지 않는다.
이러한 제한사항들이 있고, 이 제한사항 안에서 할당기 개발자는 처리량과 메모리 이용도를 최대화하려는 성능 목표를 달성하기 위해 노력한다.
첫째, 처리량 극대화. 할당기의 처리량은 단위 시간당 완료되는 요청의 수로 정의된다. 이를 극대화히기 위해서는 할당과 반환 요청들을 만족시키기 위한 평균 시간을 최소화해서 처리량을 최대화하면 된다.
둘째, 메모리 이용도 최대화. 가상메모리는 무한 자원이 아니다. 한 시스템에서 모든 프로세스에 의해 할당된 가상메모리의 양은 디스크 내의 swap 공간의 양에 의해 제한된다. 즉, 우리는 가상메모리가 유한 자원이라는 점을 인식해야 한다. 이는 큰 크기의 메모리 블록을 할당하고, 반환할 것을 요청받는 동적 메모리 할당기의 경우에 특히나 그러하다. 할당기가 힙을 효율적으로 사용하는지 측정하는 기준으로 peak utilization이 있다. 만약 n개의 배열을 할당했다고 하자. 이때 어떤 응용 프로그래밍 p 바이트의 블록을 요청하면, 할당된 블록은 데이터 p 바이트를 갖는다. 그리고 요청 R_k 가 완료된 후에 종합 데이터 P_k는 현재 할당된 블록들의 데이터들의 합이고 되고, H_k는 현재 힙의 크기를 나타낸다. 그러면 k 요청에 대한 최고 이용도는 U_k로 나타내며, 다음과 같은 식이 완성된다.
U_k = max_i<=k P_i / H_k
할당기의 목적은 최고 이용도 U_n-1을 전체 배열에 대해서 최대화하는 것이다.
이렇듯 처리량과 이용도 사이에는 trade off 가 존재하고, 우리는 이 2가지 목표 사이에 적절한 균형을 찾는 것이 중요하겠다.
단편화
가용 메모리에 할당이 불가한 경우가 있는데, 이를 단편화라고 하고, 여기에는 2종류의 단편화가 있다.
우선 내부 단편화는 할당된 블록이 데이터 자체보다 더 클 때 발생한다. 이 정렬 제한사항을 만족시키기 위해서 할당기는 블록의 크기를 padding을 이용해서 증가시킬 수 있다.
그 다음 외부 단편화는 할당 요청을 만족시킬 수 있는 메모리 공간이 전체적으로는 공간을 모았을 때 충분한 크기가 존재하지만, 현재 요청을 처리할 수 있는 단일 가용 블록은 없는 경우에 발생한다. 이 측정하기도 어렵고, 예측이 불가능한 외부 단편화때문에 할당기들은 더 적은 수의 더 큰 가용 블록들을 유지하는 방법을 채택한다.
구현 이슈
가장 간단히 상상할 수 있는 할당기는 힙을 하나의 커다란 바이트 배열과 이 배열의 첫 번째 바이트를 가리키는 포인터 p로 구성할 수 있겠다. 여기서 size 바이트를 할당하기 위해서 malloc은 현재 p값을 스택에 저장하고, p를 size 크기만큼 증가시키고, p의 이전 값을 호출자에게 반환한다. 그리고 free는 아무것도 하지않고, 단순히 호출자에게 반환한다. 이렇게하면 malloc과 free가 적은 수의 instruction을 실행하기 때문에 처리량은 매우 좋다. 하지만 할당기가 블록들을 하나도 재사용하지 않기 때문에 메모리 이용도는 매우 나쁠 것이다.
따라서 처리량과 이용도 사이에 좋은 균형을 갖는 실용적인 할당기는 다음 이슈들을 고려해야 한다.
- 가용 블록 구성 : 어떻게 가용 블록을 지속적으로 추적하는지
- 배치 : 새롭게 할당된 블록을 배치하기 위한 가용 블록을 어떻게 선택하는지
- 분할 : 새롭게 할당한 블록을 가용 블록에 배치한 후에 가용 블록의 나머지 부분들로 무엇을 할 것인지
- 연결 : 방금 반환된 블록으로 무엇을 할 것인지
여기서 기본적인 배치, 분할, 연결 기술들은 서로 다른 가용 블록 구조와 관련되고, 이들을 묵시적 가용 리스트로 알려진 간단한 가용 블록 구조의 context에서 소개한다.
정렬 제한 조건
정렬 제한 조건이란 할당기에 블록을 할당 시에 블록들이 가지는 바이트의 수가 정렬 조건의 배수가 되게 하는 것이다. 즉, 더블 워드 정렬 조건으로 정렬이 이루어진다고 가정하자. 그러면 만약 8바이트의 데이터를 확보했다면, 헤더 4바이트 + 데이터 8바이트가 되어서 12 바이트가 필요한데, 더블 워드 정렬 조건으로 바이트의 수가 8의 배수가 되어야 하므로, 이때 패딩을 4바이트 하나를 추가하여 8의 배수를 맞추는 것이다.
헤더의 하위 3비트
그럼 '더블 워드의 정렬 제한 조건이 맞다면, 블록 크기는 항상 8의 배수이고, 하위 3비트는 항상 0이다.' 이 말을 한번 이해해보자. 이에 앞서 먼저 기억해야 하는 2가지는 다음과 같다.
- 헤더는 1워드로 4바이트이다.
- 더블 워드 정렬로 블록의 크기는 항상 8의 배수이다.
이때, 헤더의 32비트에는 블록의 사이즈가 저장된다. 그리고 하위비트 3개까지는 십진수로 나타냈을 때, 최대 7까지 나타낼 수 있다. 그렇기 때문에 8의 배수가 헤더에 저장되면, 4번째 비트부터 변화가 생기고 하위 3개의 비트는 항상이 0이 된다. 그래서 이 하위 3개 비트 중 가장 오른쪽을 Allocated(1), Free(0) 여부 기록용으로 사용한다.
묵시적 가용 리스트
모든 실용적인 할당기는 블록 경계를 구분하고, 할당된 블록과 가용 블록을 구분하는 데이터 구조를 필요로 한다. 그리고 대부분의 할당기는 이 정보를 블록 내에 내장한다. 이 방법에서 한 블록은 1워드 헤더, 데이터, 추가적인 패딩으로 구성된다. 헤더는 블록 크기와 블록이 할당되었는지 혹은 가용 상태인지를 인코딩한다. 1이면, allocated. 0이면, free이다.
아래 그림은 Implicit Free List Block 구조인데, Header, Payload, Padding으로 구성되어 있다. 이때, Padding은 Double Word(8byte) 정렬 제한 조건을 사용할 경우에 블록의 크기는 항상 8의 배수이어야 하는데, 이러한 제한 조건을 지키기 위해서 추가되어 진다. 즉, 외부 단편화를 극복하는 전략 중 하나라고 생각하면 된다. 그 밑에는 메모리 블록과 힙 구조를 추상화해서 나타낸 그림이다. 각 블록 1칸은 1워드(4바이트)를 의미하며, Double Word 정렬 제한 조건에 따라 Implicit Free List가 힙에 올라간 상태를 보여준다.
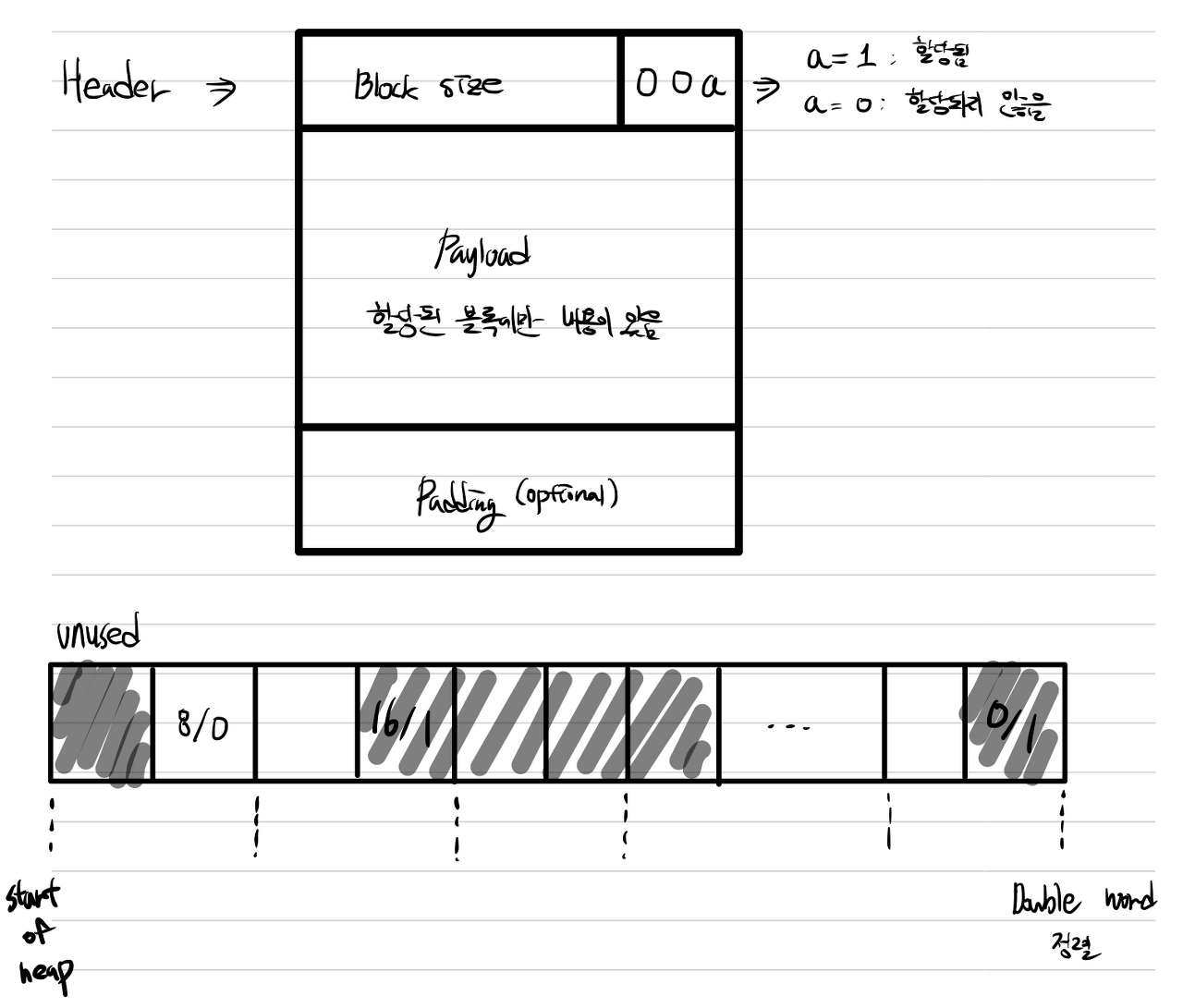
이러한 구조를 묵시적 리스트라고 하는데, 가용 블록이 헤더 내 필드에 의해서 묵시적으로 연결되기 때문이다. 이렇게 할당기는 간접적으로 가용 블록 전체 집합을 힙 내의 전체 블록을 다니면서 방문할 수 있다. 이런 묵시적 가용 리스트의 장점은 단순성이다. 반면에 단점은 할당된 블록을 배치하는 것과 같은 가용 리스트를 탐색해야 하는 연산들의 비용이 힙에 있는 전체 할당된 블록과 가용 블록의 수에 비례한다는 것이다. 여기서 시스템의 정렬 요구조건과 할당기의 블록 포맷 선택이 할당기에 최소 블록 크기를 결정한다는 것을 숙지하자. 즉, 할당되거나 반환된 블록 모두 이 최소값보다 더 작을 수는 없다.
어플리케이션이 k바이트의 블록을 요청할 때, 할당기는 요청한 블록을 저장하기에 충분히 큰 가용 블록을 리스트에서 검색하는데, 할당기가 이 검색을 수행하는 방법에는 first fit, next fit, best fit이 있다. 그리고 연구 결과에서 일반적으로 best fit이 first fit이나 next fit보다 더 좋은 메모리 이용도를 갖는다는 것을 밝혔다. 하지만 묵시적 가용 리스트 같은 단순한 가용 리스트 구성을 사용하여 best fit을 사용하면 단점이 힙을 완전히 다 검색해야 한다는 점이 있다. 그래서 힙을 모두 검색하지 않는 best fit 정책을 단순화한 segregated free list에 대해 좀 더 살펴봐야 한다.
할당기가 크기가 맞는 가용 블록을 찾은 후에는 가용 블록의 어느 정도를 할당하지에 대한 정책적 결정을 내려야 한다. 그런데 만일 할당기가 요청한 블록을 찾을 수 없다면 어떻게 될까? 외부 단편화가 발생한다. 이럴 때 한 가지 옵션은 메모리에서 물리적으로 인접한 가용 블록들을 합쳐서 더 큰 가용 블록을 만들어보는 것이다. 그런데도 해결이 안되면 할당기는 커널에게 sork 함수를 호출해서 추가적인 힙 메모리를 요청한다. 할당기는 추가 메모리를 한 개의 더 큰 가용 블록으로 변환하고, 이 브록을 가용 리스트에 삽입한 후에 요청한 블록을 이 새로운 가용 블록에 배치한다.
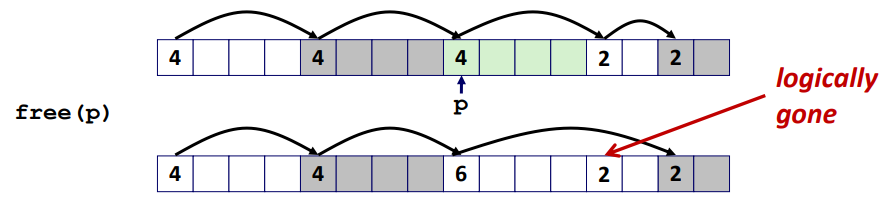
할당기가 할당한 블록을 반환할 때, 새롭게 반환하는 블록에 인접한 다른 가용 블록들이 있을 수 있다. 이러한 인접 가용 블록들은 false fragmentation이라는 현상을 유발할 수 있고, 그럼 다음과 같이 작고 사용할 수 없는 가용 블록들은 쪼개진 많은 가용 메모리로 존재할 수 있게 된다. 이러한 false fragmentation을 극복하기 위해서 실용적인 할당기라면 coalescing이라는 과정으로 인접 가용 블록들을 통합해야 한다. 할당기는 블록이 반환될 때마다 인접 블록을 통합해서 즉시 연결을 선택할 수도 있고, 또는 일정 시간 후에 가용 블록들을 연결하기 위해 기다리는 지연 연결을 선택할 수도 있다. 지연 연결은 일부 할당 요청이 실패할 때까지 연결을 지연하고, 그 후에 전체 힙을 검색해서 모든 가용 블록들을 연결한다. 반면에 즉시 연결은 간단하고, 상수 시간 내에 수행할 수 있지만, 일부 요청 패턴에 대해서는 블록이 연속적으로 연결되고, 잠시후에 분할되는 Thrashing의 형태를 유발할 수 있다. 그래서 빠른 할당기들은 종종 지연 연결의 형태를 선택한다.
경계 태그로 연결하기
그럼 할당기는 어떻게 연결을 구현할까?
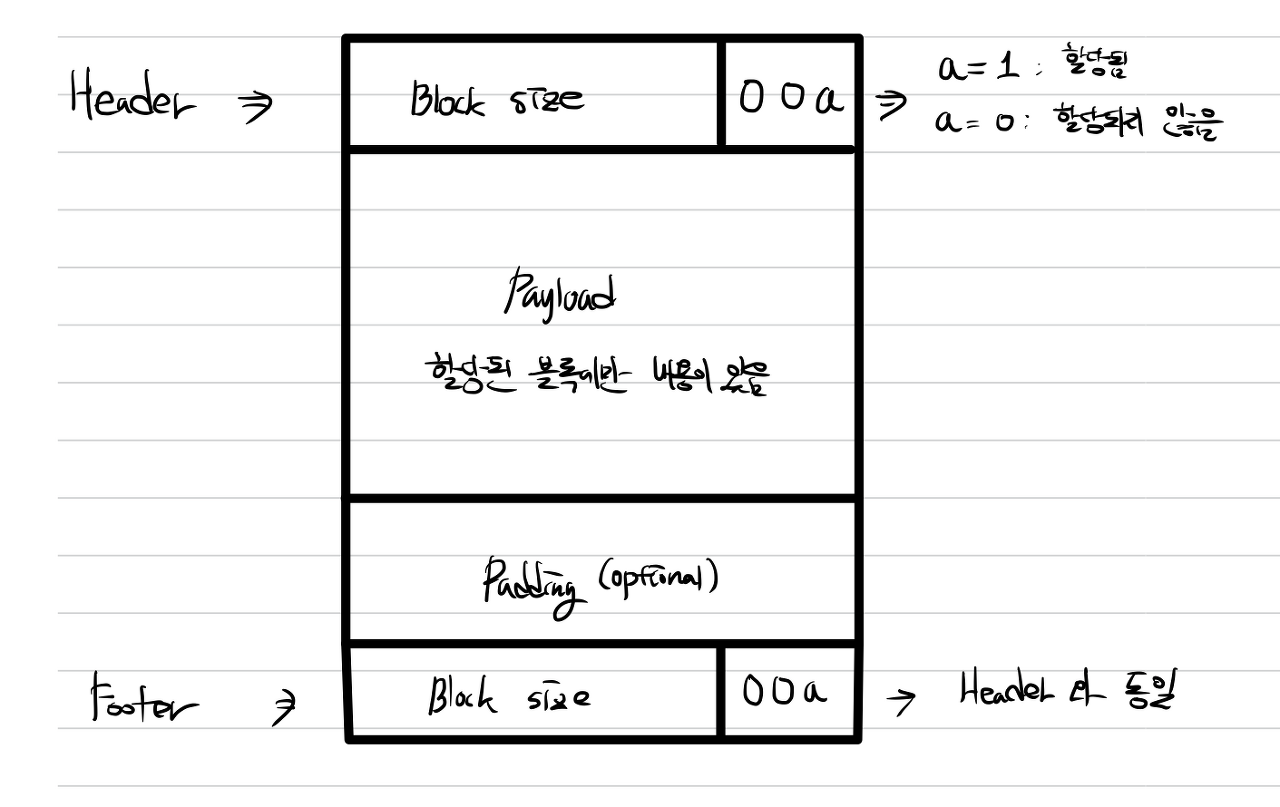
원래 이전 블록을 현재 블록과 연결하기 위해서는 블록의 header에 크기와 가용 여부에 대한 정보가 있는 상태이기 때문에, 이전 블록이 가용 가능한지 판단하기 위해서 이전 블록의 헤더 위치를 찾아야했다. 이 방법은 선형 탐색시간이 걸리게 된다. 하지만 footer를 추가함으로써 현재 블록과 이전 블록을 연결할 때, 현재 블록의 헤더 바로 앞이 이전 블록의 footer이고, 이 footer를 통해 이전 블록의 크기를 알 수 있고, 이전 블록의 시작 위치를 알 수 있음이 보장된다. 이렇게 각 블록의 끝 부분에 헤더와 동일한 정보인 사이즈, 가용여부를 가지는 footer라는 1워드 크기의 공간을 할당해주는데, 이를 경계 태그라고 한다. 정리하면, 이렇게 함으로써 현재 블록과 이전 블록을 연결할 때, 현재 블록 헤더의 바로 앞이 이전 블록의 풋터이고, 이를 이용해서 이전 블록의 크기를 알 수 있고, 이전 블록의 시작 위치를 알 수 있음이 보장된다. 이를 통해서 다음 블록뿐만 아니라 이전 블록과의 연결도 상수 시간 내에 완료할 수 있게 된다. 경계 태그를 포함한 Implicit Free List Block의 구조는 다음과 같다.
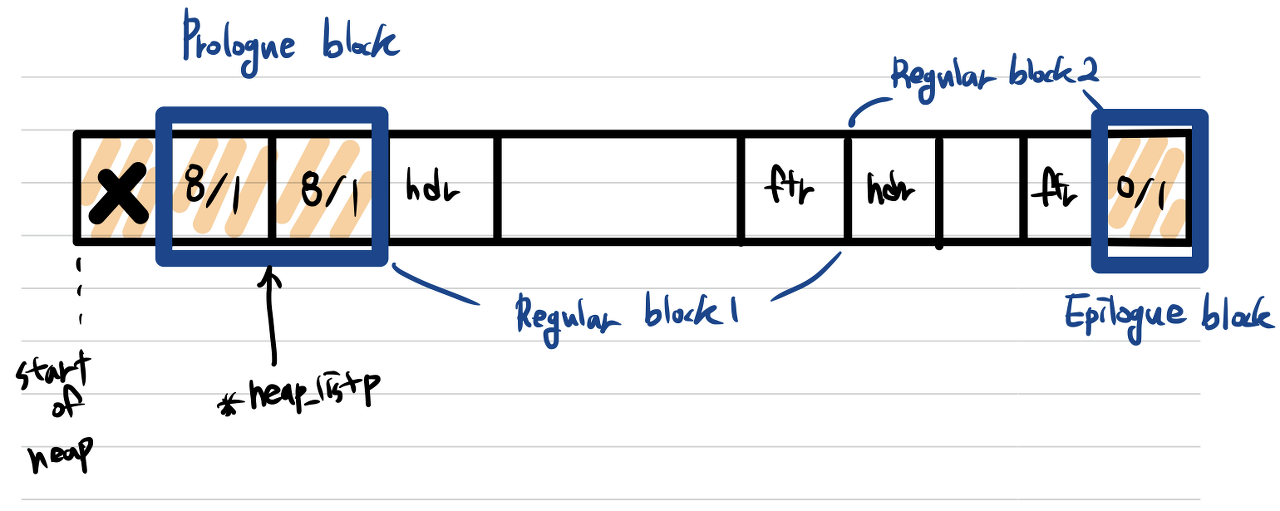
이 블록이 heap에 할당되면, 아래 그림과 같이 추상화할 수 있게 된다. 여기서 prologue block(prologue header, prologue footer)와 epilogue block(epilogue header)는 각각 힙의 시작과 끝을 알려주는 블록으로, 연결 과정 구현에 있어서 가장자리 조건을 없애주기 위한 속임수라고 볼 수 있다.
그럼 할당기가 현재 블록을 반환할 때, 가능한 모든 경우들을 생각해보자.
우선 첫 번째로 이전과 다음 블록이 모두 할당되어 있는 경우, 현재 블록의 상태는 할당에서 가용으로 변경된다.
두 번째로 이전 블록은 할당상태이고, 다음 블록은 가용상태인 경우, 현재 블록은 다음 블록과 통합된다. 즉, 현재 블록과 다음 블록의 footer는 현재와 다음 블록의 크기를 합한 것으로 갱신된다.
세 번째 이전 블록은 가용상태이고, 다음 블록은 할당상태인 경우, 이전 블록은 현재 블록과 통합된다. 즉, 이전 블록의 헤더와 현재 블록의 footer는 두 블록의 크기를 합한 것으로 갱신된다.
네 번째 이전 블록과 다음 블록이 모두 가용상태인 경우, 세 블록은 모두 하나의 하나의 가용 블록으로 통합되고, 이전 블록의 header와 다음 블록의 footer는 세 블록의 크기를 합한 것으로 갱신된다. 그리고 각각의 경우에 연결은 상수 시간에 이루어진다.
이렇게 경계 태그 아이디어는 여러 가지 유형의 할당기와 가용 리스트 구성에도 일반화될 수 있는 간단하고도 우아한 개념이다. 하지만 여기에도 잠재적인 단점이 존재하는데, 각 블록이 header와 footer를 유지해야 하므로 memory overhead가 발생할 수 있다는 점이다.
그렇기에 footer가 할당된 블록에 있을 필요를 없애는 최적화 방법이 존재하는데, 현재 블록을 메모리에 있는 이전과 다음 블록과 연결하려고 할 때, 만일 이전 블록이 가용한 경우에만 이전 블록의 footer에 있는 size 필드가 필요하다는 점을 기억하게 하면 된다. 즉, 현재 블록의 추가적인 하위 비트들 중 하나에 이전 블록의 할당/가용 비트를 저장하려고 하면, 할당된 블록들은 footer가 필요 없어지고, 이 추가적인 공간을 데이터를 위해 사용할 수 있다. 하지만 가용 블록은 여전히 footer를 필요로 한다는 점에 유의해야 한다.
'컴퓨터 사이언스 > 운영체제' 카테고리의 다른 글
| Explicit Allocator - Explicit Free List (0) | 2023.11.15 |
|---|---|
| 인터럽트와 시스템 콜 (0) | 2023.11.15 |
| demand-zero memory (0) | 2023.11.15 |
| DMA (0) | 2023.11.14 |
| 동적 메모리 할당기 구현 (1) | 2023.11.13 |
