최단 거리 알고리즘이란 그래프 상에서 노드 간의 탐색 비용을 최소화하는 알고리즘이다. 일반적으로는 네비게이션과 같은 길찾기에 적용된다. 이러한 최단 거리 알고리즘의 종류에는 크게 3가지가 있다.
다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 그래프 상의 특정 한 노드에서 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이다. 다르게 표현하면 가중 그래프에서 간선 가중치의 합이 최소가 되는 경로를 찾는 알고리즘 중 하나이다.
그래서 다익스트라는 그리디와 동적 계획법이 합쳐진 형태이다. 왜냐하면, 현재 위치한 노드에서 최선의 경로를 반복적으로 찾으면서도 계산해둔 경로를 활용해 중복된 하위 문제를 풀기 때문이다.
또한 다익스트라는 만약 그래프에 음의 가중치가 있다면 사용할 수 없다. 그 이유는 그리디를 통해 최단 경로라고 여겨진 경로 비용을 DP 테이블에 저장한 뒤 재방문하지 않는데, 만약 음의 가중치가 있다면 이러한 규칙이 어긋날 수 있기 때문이다.
따라서 음의 가중치가 포함된다면 플로이드 워셜이나 벨만 포드 알고리즘을 사용해 최단 경로를 구할 수 있다. 다만 시간 복잡도가 늘어나는 단점이 있어서 핵심은 해결하고자 문제에 따라 알맞은 알고리즘을 선택해야 한다.
그럼 이제 다음과 같은 그래프를 보고 다익스트라 알고리즘의 동작 원리를 한번 살펴보자.

최종적으로 1에서 다른 모든 노드까지의 비용은 위 테이블이 된다.
이제 이를 코드로 구현하기 위해서는 가중치에 중요도가 있으므로, 자료구조 힙을 사용해 표현해줄 수 있다.
""" This is input value. you can just copy and paste it.
5 6 1
1 2 3
1 4 8
1 5 9
2 1 2
2 3 2
3 2 2
3 4 1
3 5 3
4 1 8
4 3 1
5 1 9
"""
import heapq
import sys
def dijkstra(start):
heap = []
heapq.heappush(heap, [0, start]) # 최소힙은 배열의 첫번째 값을 기준으로 배열을 정렬한다.
INF = float('inf')
weights = [INF] * (vertex + 1) # DP에 활용할 memorization 테이블 생성
weights[start] = 0 # 자기 자신으로 가는 사이클은 없다.
while heap:
weight, node = heapq.heappop(heap)
if weight > weights[node]: # 비용 최적화 전부터 큰 비용일 경우는 고려할 필요가 없다.
continue
for n, w in graph[node]: # 최소 비용을 가진 노드를 그리디하게 방문한 경우에는 연결된 간선을 모두 확인해야 한다.
W = weight + w
if weights[n] > W: # 여러 경로를 방문해 합쳐진 가중치 W가 더 비용이 적다면
weights[n] = W # 업데이트한다.
heapq.heappush(heap, (W, n)) # 최소 비용을 가진 노드와 합쳐진 가중치를 추가한다.
return weights
vertex, edge, start = map(int, sys.stdin.readline().rstrip().split())
graph = [[] for _ in range(vertex + 1)]
for _ in range(vertex + edge):
src, dst, weight = map(int, sys.stdin.readline().rstrip().split())
graph[src].append([dst, weight])
weights = dijkstra(start)
print(weights)
플로이드-워셜(Floyd-Warshall Algorithm)
모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구하는 알고리즘이다.
그럼 다익스트라 알고리즘과의 차이를 알아보자.
우선 플로이드-워셜은 소스코드가 다익스트라에 비해 매우 짧아 구현이 쉽다.
또한 다익스트라의 경우 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 이후 해당 노드를 거쳐가는 경로를 확인하면서 최단 거리 테이블을 갱신하는 방식으로 동작한다. 물론 플로이드 워셜도 단계마다 거쳐가는 노드를 기준으로 알고리즘을 수행하지만, 매 단계마다 방문하지 않은 노드중에서 최단 거리를 갖는 노드를 찾을 필요는 없다.
그리고 다익스트라는 한 지점에서 다른 지점까지의 최단 거리이기 때문에 1차원 리스트에 최단 거리 정보를 저장하는 반면에 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다.
마지막으로 플로이드 워셜은 DP 알고리즘에 속하는 반면에 다익스트라는 그리디 알고리즘에 속한다고 볼 수 있다. 왜냐하면 만약 노드의 개수가 N개라고 할 때, N번만큼의 단계를 반복하며 점화식에 맞게 2차원 리스트를 갱신하기 때문이다.
- 플로이드 워셜 알고리즘의 시간 복잡도
플로이드 워셜 알고리즘의 시간 복잡도는 O(N^3)이 나온다. 왜냐하면, 노드의 개수가 N개일 때, N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다. 그래서 시간 복잡도가 총 O(N^3)인 것이다.
- 플로이드 워셜 알고리즘의 점화식
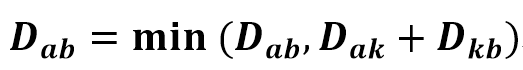
- 플로이드 워셜 동작 흐름
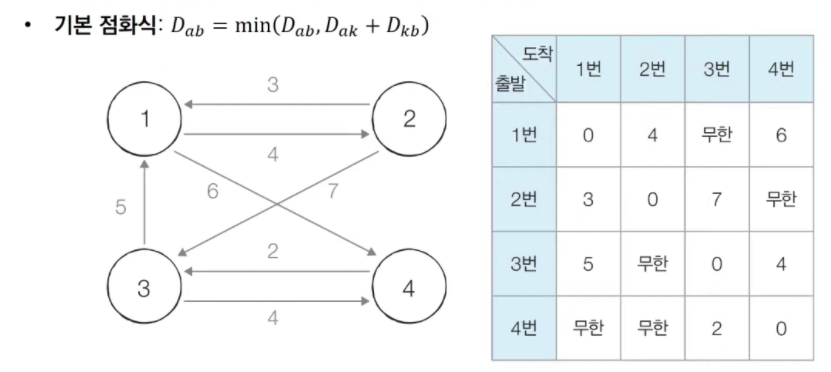
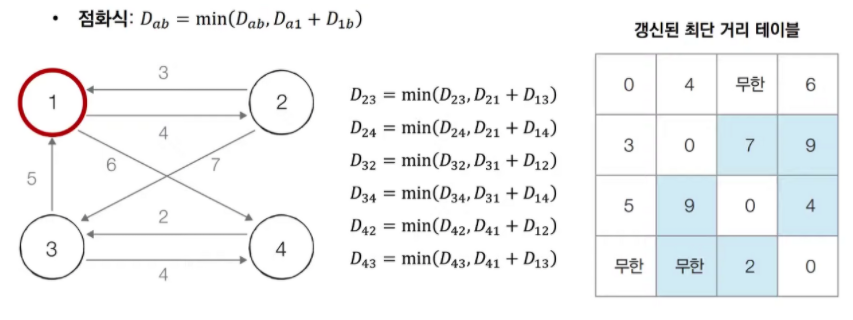

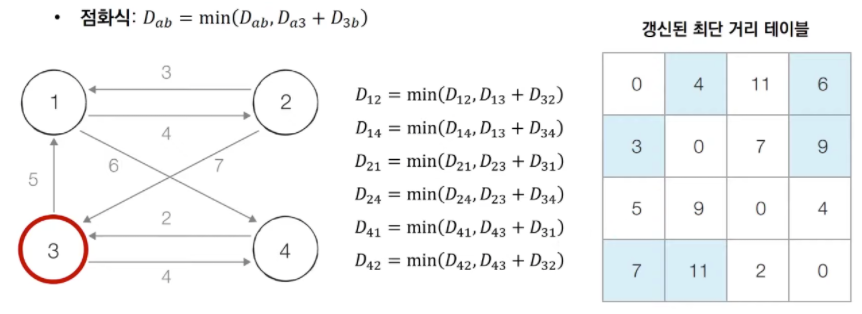
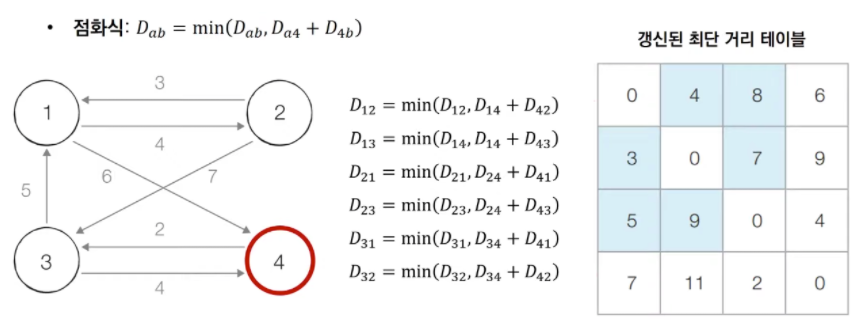
인용
'컴퓨터 사이언스 > Algorithm' 카테고리의 다른 글
| 분리 집합(Disjoint Set): Union-Find (1) | 2023.10.21 |
|---|---|
| 최소 스패닝 트리(MST. Minimum Spanning Tree) (0) | 2023.10.21 |
| 다익스트라(Dijkstra) (1) | 2023.10.19 |
| 위상 정렬 (1) | 2023.10.19 |
| Tree (1) | 2023.10.19 |
