Union-Find의 개념은 다음과 같다.
A와 B가 친구 관계에 있고, 내가 A와 친구 관계이면 자동으로 나와 B는 친구 관계가 된다. 이 개념을 이용해서 내가 A라는 사람과 친구 관계를 맺었는데, 그럼 내가 F라는 사람과 친구 관계가 될 수 있을지는 어떻게 알 수 있을까?
답은 친구 관계를 그래프로 나타낸 후에 나를 시작으로 그래프 탐색(DFS, BFS)를 통해 목표 지점까지 도달할 수 있는지 확인하면 간단할 것이다.
하지만 친구 관계는 언제나 새롭게 생겨날 수 있다. 그럼 친구 관계가 새로 생겼다고 할 때, F와 친구 관계가 될 수 있는지 알기위해서 다시 그래프 탐색을 진행해야 한다. 따라서 이런 방식을 사용하기 때문에 사용하는 사용자의 수가 엄청 많다면 새로운 친구 관계가 생겨날 때마다 그래프 탐색이 모든 사용자마다 진행되어야 하므로 매우 많은 시간이 걸릴 것이다.
그러므로 친구 관계를 그래프의 형태가 아닌 그 사람이 속해있는 그룹을 통해 표현하다면 소요되는 시간을 대폭 단축시킬 수 있을 것이다. 내가 A와 친구 관계를 맺었을 때, 나는 A와 같은 그룹에 속하게 된다. 이제 내가 다른 사용자와 친구 관계인지는 속한 그룹만 비교하면 되는 것이다. 즉, A가 속한 그룹이 Green이고, F가 속한 그룹이 Orange그룹일 때, 나와 그룹이 다르므로 그 사람은 친구 관계가 아니라는 것을 알 수 있다. 이때, 만약 Green 그룹의 한 멤버와 Orange그룹의 한 멤버가 새 친구 관계로 생성될 경우에는 두 그룹을 합침으로써 친구 관계를 갱신할 수 있다. 즉, A와 F는 이제 같은 그룹에 속하게 되고, 친구 관계가 됨을 알 수 있다.
여기까지 개념을 실생활에 빗대어 생각해봤고, 이제 핵심 주제를 한번 살펴보자.
분리 집합이란 무엇일까?
분리 집합은 서로소 집합이다. 즉, 이미 존재하는 집합 U에 대해서 겹치는 부분이 발생하지 않도록 모든 원소들을 분리한 부분집합을 말한다. 따라서 A, B 집합은 분리 집할일때 서로 공통 원소를 가지지 않는다.
Union-Find는 이러한 분리 집합을 구현하는 알고리즘으로 각 그룹을 트리의 형태로 표현한다.
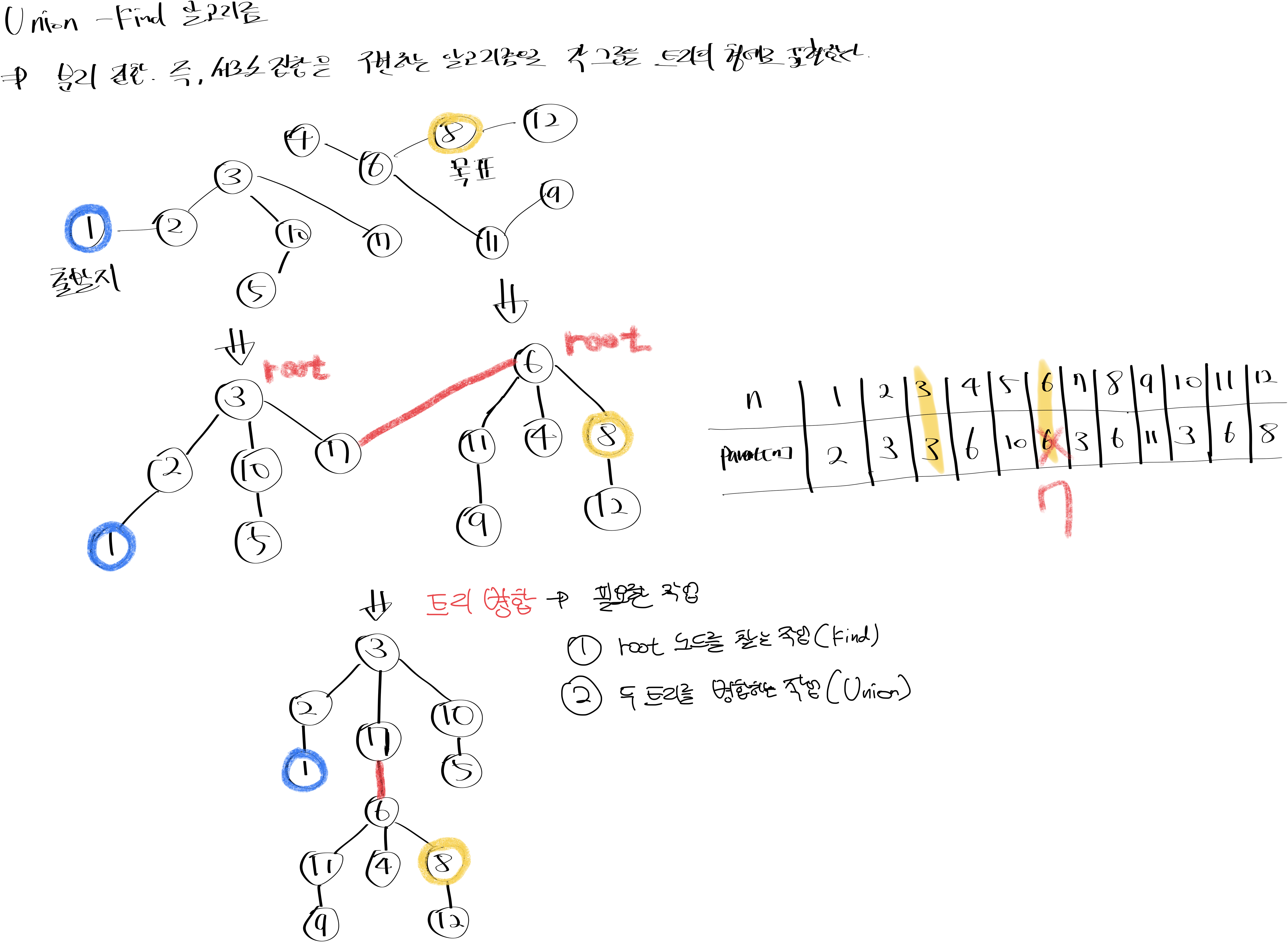
각 노드마다 그 노드의 부모 노드 번호를 기록하여 그래프를 트리 구조로 나타낼 수 있다. 이렇게 나타낸 트리는 항상 최상위 노드인 root 노드를 가지게 되는데, 바로 이 root 노드를 통해 그룹을 구별할 수 있게 된다. 따라서 만약 내가 8번 노드와 친구 관계임을 알고싶다면 내가 속한 트리의 루트와 8번 노드가 속한 트리의 루트 노드를 통해 그룹을 구별하면 된다. 이때, 표에서 루트 노드는 부모 노드를 자기 자신으로 설정한다. 아래 그림을 보면 루트가 다른 상태에서 두 노드 중 하나의 부모 노드를 다른 하나로 지정하여 다음과 같이 트리를 병합할 수 있다. 이 부분은 paraent[6]이 6에서 7로 갱신된 것을 보면 확인할 수 있다. 이렇게 되면 1과 8은 같은 그룹이 되며, 그에 따라 친구 관계가 되는 것이다.
이 union-find 기법을 사용해 최소 신장 트리 알고리즘을 풀때 적용해보면, 부모 노드가 서로 같은게 있으면 사이클이 돌기 때문에 신장 트리가 될 수 없게 된다.
따라서 이렇게 트리를 병합할 때는 다음 2단계의 작업이 필요하다.
- root 노드를 찾는 작업(Find)
- 두 트리를 병합하는 작업(Union)
기능과 구현
- getParent(parent, int x) : 특정한 노드의 부모를 찾는다.
def getParent(parent, x):
if (parent[x] == x)
return x
return parent[x] = getParent(parent, parent[x]);- unionParent(parent, a, b) : 두 부모 노드를 합치는 함수이다.
def unionParent(parent, a, b):
a = getParent(parent, a)
b = getParent(parent, b)
# 더 작은 쪽으로 부모를 합쳐준다.
if (a < b) parent[b] = a
else parent[a] = b- findParent(parent, a, b) : 같은 부모를 가지는지 확인한다.
def findParent(parent, a, b):
a = getParent(parent, a)
b = getParent(parent, b)
if a == b:
return True
return False
인용
https://4legs-study.tistory.com/94?category=886581
분리 집합 (Disjoint Set) : Union-Find
서론 다음과 같은 메신저 프로그램이 있다. "A와 B가 친구 관계이고, 내가 A와 친구 관계이면 자동으로 나와 B는 친구 관계가 된다." 이 메신저 프로그램을 통해 내가 A라는 사람과 친구 관계를 맺
4legs-study.tistory.com
'컴퓨터 사이언스 > Algorithm' 카테고리의 다른 글
| 동적 프로그래밍과 그리디 알고리즘 (0) | 2023.10.27 |
|---|---|
| Dynamic Programming (0) | 2023.10.26 |
| 최소 스패닝 트리(MST. Minimum Spanning Tree) (0) | 2023.10.21 |
| 최단 거리 알고리즘 정리 (1) | 2023.10.20 |
| 다익스트라(Dijkstra) (1) | 2023.10.19 |
