개요
효율적인 알고리즘의 설계와 분석을 위해서는 3가지 중요한 기법들을 익혀야 한다. 이 것들에는 크기 동적 프로그래밍, 그리디 알고리즘, 분할상환 분석이 있는데, 이 기법들은 좀 더 복잡하지만, 컴퓨터로 해결할 수 있는 많은 문제들을 효과적으로 공력할 수 있게 도와준다.
동적 프로그래밍은 일반적으로 최적해(optimal solution)에 도달하기 위해 일련의 선택이 이루어지는 최적화 문제에 적용된다. 그리고 각각의 선택을 하는 과정에서 종종 같은 형태의 부분 문제가 생긴다. 동적 프로그래밍은 어떤 부분 문제가 둘 이상의 부분적인 선택 집합에서 발생하는 경우에 효과적이다. 또한 이 기법의 중요한 특징은 부분 문제의 해가 다시 나타나는 경우를 대비해 그 해를 저장해두는 것이다.
그리디 알고리즘도 동적 프로그래밍 알고리즘과 마찬가지로 일반적으로 최적해에 도달하기 위해 일련의 선택이 이루어지는 최적화 문제에 적용된다. 다만, 그리디 알고리즘의 아이디어가 다른점은 지역적으로 각각의 선택을 한다는 것이다. 간단한 예로 동전 바꾸기 문제에서 주어진 금액을 거스름 돈으로 줄 때, 동전의 개수를 최소화하기 위해 반복적으로 남은 금액보다 크지 않으면서 액수가 가장 큰 동전을 선택하면 된다. 그리고 그리디 알고리즘은 이런 많은 문제에서 동적 프로그래밍 알고리즘보다 최적해를 더 빨리 찾아낸다. 그러나 문제점이 있다. 그리디 알고리즘은 이 알고리짐이 효과적인 확인하는 일을 거쳐야 하고,이 과정이 쉽지 않을 수 있다. 이에 그리디 알고리즘이 최적해를 찾음을 보이는 수학적 기초를 제공하는 매트로이드 이론을 다룬다.
동적 프로그래밍
동적 프로그래밍을 이해하기 위해서는 우선 분할정복의 개념을 알아야 한다.
프로그래밍을 공부하다가 보면 재귀적인 구조를 가진 유용한 알고리즘이 많다. 이러한 알고리즘에서는 주어진 문제를 풀기위해 자기 자신을 재귀적으로 여러 번 호출함으로써 밀접하게 연관된 부분 문제를 다룬다. 그리고 이런 알고리즘들은 전형적으로 분할정복 접근법을 따른다. 먼저 전체 문제를 원래 문제와 유사하지만 크기가 작은 몇 개의 부분 문제로 분할하고, 부분 문제를 재귀적으로 푼다. 그런 다음 찾은 해를 결합해서 원래 문제의 해를 만들어낸다.
분할정복은 재귀 호출을 하는 각 단에서 다음 3가지 단계로 구성된다.
- 분할: 현재 문제를 같은 문제를 다루는 다수의 부분 문제로 분할
- 정복: 부분 문제를 재귀적으로 풀어서 정복
- 결합: 부분 문제의 해를 결합하여 원래 문제의 해가 되도록 만듦
그리고 병합 정렬은 분할정복 기법을 아주 잘 이용한다.
- 분할: 정렬할 n개 원소의 배열을 n/2개씩 부분 수열 두 개로 분할한다.
- 정복: 병합 정렬을 이용해 두 부분 배열을 재귀적으로 정렬한다.
- 결합: 정렬된 두 개의 부분 배열을 병합해 정렬된 배열 하나로 만든다.
이렇듯 분할 정복을 정의할 수 있는데, 이 때 부분 문제가 재귀적으로 풀 수 있을만큼 충분히 클 때를 재귀 대상이라고 한다. 그리고 만약 부분 문제가 충분히 작아져 더 이상 재귀 호출을 할 수 없을 때 '재귀가 바닥을 쳤다'고 하고, 베이스 케이스까지 내려왔다고 한다.
또한 입력의 크기가 더 작은 완전히 동일한 부분 문제 외에 원래의 문제와 다른 부분 문제를 풀어야 할 때도 있다. 그런 부분 문제는 결합 단계의 일부로 간주한다.
그리고 분할정복 체계는 점화식과 관련이 많다. 점화식이란 더 작은 입력에 대한 자신의 값으로 함수를 나타내는 방정식 또는 부등식이다. 점화식을 통해 분할정복 알고리즘의 수행 시간을 자연스럽게 표현할 수 있기 때문이다.
즉, 분할정복 알고리즘을 정리하면 문제를 서로 겹치지 않는(disjoint) 부분 문제로 분할하고, 해당 부분 문제를 재귀적으로 해결한 후, 해결 결과를 결합하여 원래의 문제를 해결한다.
그럼 이제 다시 동적 프로그래밍으로 돌아와보자.
동적 프로그래밍은 부분 문제가 서로 중복될 때, 즉 부분 문제가 다시 자신의 부분 문제를 공유할 때 적용할 수 있다. 즉, 분할정복 알고리즘의 경우에는 공유되는 부분 문제를 반복적으로 해결하여 일을 필요 이상으로 더 많이 하게되는데, 동적 프로그래밍 알고리즘을 이용하면 모든 부분 문제를 한번만 풀어 그 해를 테이블에 저장함으로써 각 부분 문제를 풀 때마다 다시 계산하는 일을 피할 수 있다. 그래서 일반적으로 최적화 문제(optimization problem)에 동적 프로그래밍을 적용한다.
다만, 여기서 주의할 점이 있는데, 이런 문제는 다양한 해를 가질 수 있다는 것이다. 그리고 각 해는 값을 가지기 때문에 이 중에서 최적의 값인 해를 찾아야한다. 따라서 이런 해를 그 문제에 대한 유일한 최적해라고 하지 않고, 한 개의 최적해라고 한다. 왜냐하면 최적의 값을 가지는 해가 여러 개 있기 때문이다.
그럼 동적 프로그래밍 알고리즘을 개발할 때 통상적으로 따르는 4단계 프로세스를 살펴보자.
- 최적해의 구조의 특징을 찾는다.
- 최적해의 값을 재귀적으로 정의한다.
- 최적해의 값을 일반적으로 bottom-up 방법으로 계산한다.
- 계산된 정보들로부터 최적해를 구성한다.
하지만 동적 프로그래밍을 사용하면 부분 문제의 해를 나중에 다시 구할 때 다시 계산하지 않고 저장된 값을 참조만하도록 그 해를 저장하기 때문에 시간과 메모리 사이에 트레이드 오프가 발생한다. (time memory trade-off).
동적 프로그래밍 방법을 구현하는데는 보통 2가지 방법이 존재한다.
첫 번째 방법은 메모하기를 이용한 하향식이다. 이 방법은 재귀 방법으로 구현하고, 각각의 부분 문제의 결과를 보통 배열이나 해시 테이블에 저장한다. 그리고 어떤 부분 문제를 이전에 풀었는지 알아보기 위해 확인한다. 만약 이전에 풀었다면 그 저장된 결과를 리턴하여 이후에 계산하는 것을 절약한다. 그러면 이 재귀 프로시저가 Memoization되었다고 말할 수 있다. 즉, 이 procedure는 이전에 이미 계산된 결과를 기억한다.
두 번째 방법은 상향식 방법이다. 이 방법은 부분 문제의 크기라는 자연스러운 개념을 따르는데, 특정 부분 문제를 푸는 것이 더 작은 부분 문데를 푸는 것에만 의존하게 한다. 즉, 부분 문제를 크기별로 정렬한 후, 가장 작은 것을 첫 번째로 하여 크기 순으로 푼다. 그래서 특정 부분 문제를 풀 때는 그 해에 영향을 미치는 더 작은 부분 문제를 모두 풀어 그 해를 저장해놓는다. 그러므로 각 부분 문제는 한 번만 풀고, 새로 등장하는 부분 문제에 필요한 모든 부분 문제는 이미 다 풀어놓은 상태가 되는 것이다.
부분 문제 그래프
동적 프로그래밍 문제에 대해 생각할 때는 관련된 부분 문제의 집합과 부분 문제가 서로 어떻게 연관되어 있는지를 이해해야 한다. 이때, 문제에 대한 부분 문제 그래프는 이런 정보를 정확하게 나타내준다.
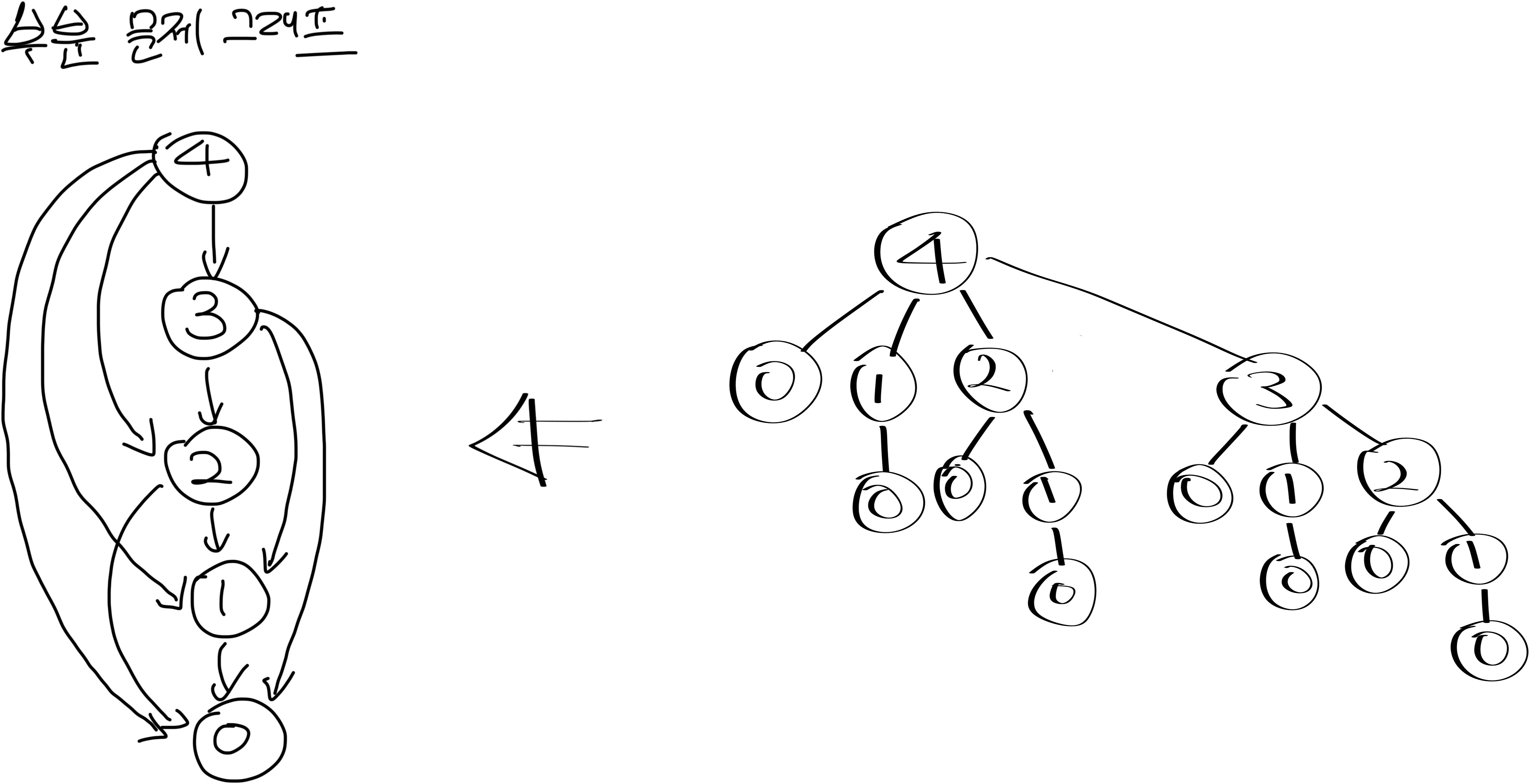
위의 부분 문제 그래프를 보면, 방향성 그래프로 각각의 다른 문제에 대해 정점 하나를 가진다. 부분 문제 x의 최적해를 결정하는 부분 문제 y에 대한 최적해를 직접적으로 참조하면, 부분 문제 그래프는 부분 문제 x에 대한 정점에서 에서 부분 문제 y에 대한 정점으로 방향성 간선을 가진다.
동적 프로그래밍의 요소
필자는 동적 프로그래밍이 그래서 언제, 어떤 문제에 적용해 해를 찾아야 할까? 하는 의문을 갖고 있었다. 따라서 최적화 문제에 동적 프로그래밍을 적용하기 위해서 가져야하는 2가지 중요한 구성 요소. 즉, 최적 부분 구조와 중복되는 부분 문제에 대해 살펴보자.
최적 부분 구조(Optimal Substructure: 문제의 최적해가 부분 문제의 최적해들로 구성되는 것을 의미)
동적 프로그래밍을 이용해 최적화 문제를 풀기 위해서 가장 먼저 할 일은 최적해의 구조의 특징을 살펴보는 것이다. 문제의 최적해가 그 안에 부분 문제의 최적해를 포함하고 있을 때, 그 문제는 최적 부분 구조를 가진다. 즉, 어떤 문제가 최적 부분 구조(optimal structure)를 가진다는 것은 동적 프로그래밍이 적용될 수 있는 좋은 밑바탕이 될 수 있다. 따라서 동적 프로그래밍은 부분 문제의 최적해로부터 전체 문제의 최적해를 구한다. 또한 고려하고 있는 부분 문제가 최적해를 구하는데 사용되는 부분 문제를 모두 포함하는지를 확인해야 한다.
중복되는 부분 문제(Overlapping Subproblem: 부분 문제에 대해서 한 번만 연산하고 결과를 저장. 이 저장한 값을 재활용하여 따로 중복되는 문제에 대한 연산을 할 필요가 없으므로 효율적임)
두 번째 요소는 부분 문제들의 범위가 작아야 한다는 것이다. 이는 재귀 알고리즘을 사용하면 항상 새로운 부분 문제를 계속 만들어 풀기보다는 같은 문제를 반복해서 풀게 된다는 것을 말한다. 즉, 재귀 알고리즘이 같은 문제를 계속 반복해서 풀게되는 경우, 그 최적화 문제가 중복되는 부분 문제(overlapping subproblems)를 가진다고 말한다. 이와 반대로 분할정복 기법(divide and conquer)를 사용하기에 적합한 문제는 보통 재귀적으로 호출하는 매 단계마다 중복되지 않는 새로운 문제를 만든다. 정리하면 동적 프로그래밍 알고리즘은 중복되는 부분 문제를 이용하고, 각 부분 문제를 한번만 계산하고 그 해를 테이블에 저장해서, 그 부분 문제가 중복되어 나올때 상수 시간에 테이블을 찾아봄으로써 해를 얻는다. 이렇게 동적 프로그래밍을 이용하면 테이블에 있는 각 부분 문제에서 어떤 선택을 했는지 저장하여 이 정보를 테이블에 저장해놓은 비용들로부터 재구성하지 않아도 되게 해준다. (최적해의 재구성). 따라서 각 부분 문제를 풀때, 어떤 선택을 했는지 O(1) 시간에 재구성할 수 있다.
memoization vs tabulation
하향식 동적 프로그래밍 기법에 적용되는 memoization 방법과 상향식 동적 프로그래밍 기법에 적용되는 tabulation 방법의 차이점을 알아보자. 모든 부분 문제를 적어도 한번씩 풀어야한다면, 상향식 동적 프로그래밍이 그에 해당하는 하향식 memoization 알고리즘보다 반복되는 재귀 호출을 위한 부담이 없고,테이블을 유지하는데 드는 비용도 적어 상수배만큼 더 빠른 수행시간을 보인다. 게다가 어떤 문제들에서는 필요한 시간이나 공간을 좀 더 줄일 수 있도록 하기 위해 동적 프로그래밍 알고리즘에서 테이블을 접근하는 일정한 패턴을 이용할 수도 있다. 그러나 일부의 부분 문제들의 해가 필요없다면 필요한 부분 문제만 계산하는 memoization 알고리즘이 더 유리할 것이다.
Longest Common Subsequence (LCS)
LCS라는 약어는 주로 Longest Common Subsequence를 말하지만, Longest Common Substring을 말하기도 한다.
그럼 둘의 차이점은 무엇일까? 문자열 ABCDEF와 GBCDFE를 이용하여 차이점을 예시로 들어보면 Longest Common Subsequence는 BCDF, BCDE가 될 수 있다. 즉, 부분수열이기 때문에 문자 사이를 건너뛰어 공통되면서 가장 긴 부분 문자열을 찾으면 된다. Longest Common Substring은 BCD인데, 부분 문자열이 아니기 때문에 한번에 이어져있는 문자열만 가능하다.
그럼 먼저 Longest Common Substring을 먼저 알아보도록 한다.
우선 최장 공통 문자열의 점화식을 코드로 작성해보면 다음과 같다. LCS라는 2차원 배열 이용해 두 문자열을 행, 열에 매칭한다. i, j가 0일 때는 모두 0을 넣어줘 마진값을 설정하고, 이후로 i, j가 1이상일 때부터 검사를 시작한다.
import sys
input = lambda: sys.stdin.readline().rstrip()
string_A = input()
string_B = input()
LCS = []
for i in range(len(string_A)):
for j in range(len(string_B)):
if i == 0 and j == 0:
LCS[i][j] = 0
elif string_A[i] == string_B[j]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = 0
그러면 다음과 같이 테이블이 만들어지고 채워지면서 가장 긴 부분 문자열이 도출된다.

그렇다면 이번에는 다른 LCS인 Longest Common Subsequence를 만들어보자.
만드는 방법은 위와 마찬가지로 LCS라는 2차원 배열에 매핑하고 마진값을 설정한 후에 검사한다.
- 문자열A와 문자열B의 한 글자씩 비교해본다.
- 두 문자가 다르다면 LCS[i - 1][j]와 LCS[i][j - 1] 중에 큰 값을 표시한다.
- 두 문자가 같다면 LCS[i - 1][j - 1] 값을 찾아 +1 한다.
- 위 과정을 반복한다.
import sys
input = lambda: sys.stdin.readline().rstrip()
string_A = input()
string_B = input()
LCS = [[] * len(string_A) for _ in range(len(string_B))]
for i in range(len(string_A)):
for j in range(len(string_B)):
if i == 0 and j == 0:
LCS[i][j] = 0
elif string_A[i] == string_B[j]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])
이전의 공통 문자열을 구하는 부분과 달라진 부분은 비교하는 두 문자가 다를 때인데, 비교하는 두 문자가 같을 때는 같은 과정을 보여준다. 그렇다면 달라진 부분에 대해 좀 더 자세히 알아보자.
부분 수열은 연속된 값이 아니다. 따라서 현재 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속해서 유지가 된다. 이때, 현재의 문자를 비교하는 과정 이전의 과정이 바로 LCS[i - 1][j]와 LCS[i][j - 1]이다. 즉, AB와 GBC의 최장 공통 부분수열을 B를 구하기 위해서는 문자열 A와 GBC를 비교하는 과정과 문자열 AB와 GB를 비교하는 과정이 필요하다. 그리고 문자열 AB와 GB를 비교하는 과정에서 최대 공통 부분수열이 B임을 확인했기 때문에 AB와 GBC의 최대 공통 부분수열 역시 B가 되는 것이다.

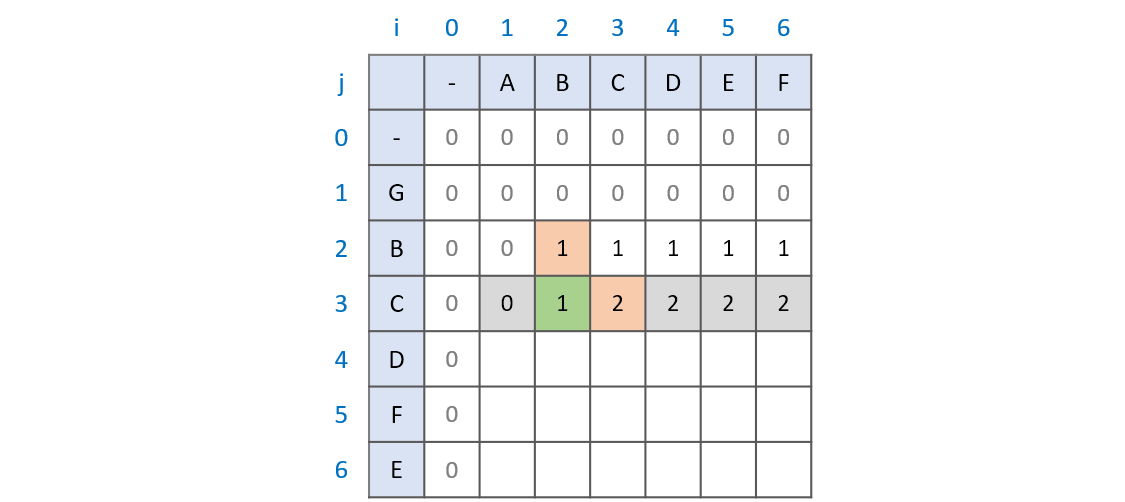
그리고 Longest Common Subsequence 또한 비교하는 문자가 같으면 LCS[i][j] = LCS[i - 1][j - 1] + 1 의 과정을 거치는데 왜 그럴까? 그 것은 두 문자가 같은 상황이 오면 지금까지의 최대 공통 부분수열에 1을 더해주는 개념이 적용된 것이다. 즉, ABC와 GBC를 비교한다고 할때, LCS 배열은 LCS[i -1][j]와 LCS[i][j - 1]의 비교를 통해 언제나 본인까지의 최대 공통 부분수열 값을 가지고 있다. 문자열 AB와 GB와 문자열 ABC와 GBC를 비교할 때 달라진 점은 두 문자열 모두 C가 추가된 점이다. 그래서 기존의 최대 공통 부분수열인 B에 C를 더한 BC가 최대 공통 부분수열이 되는 것이다.

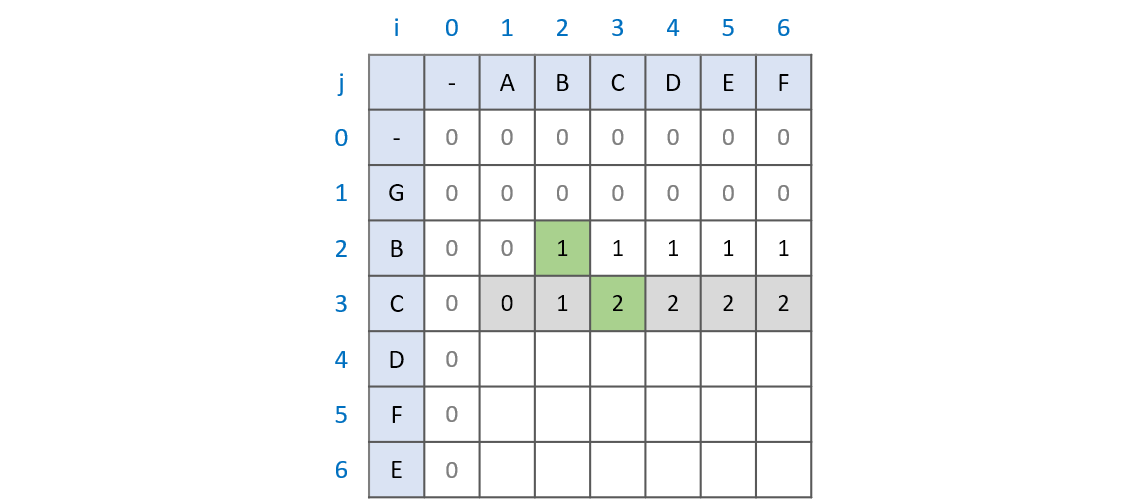
이렇게 Longest Common Subsequence를 찾아서 테이블을 다음과 같이 완성할 수 있다.
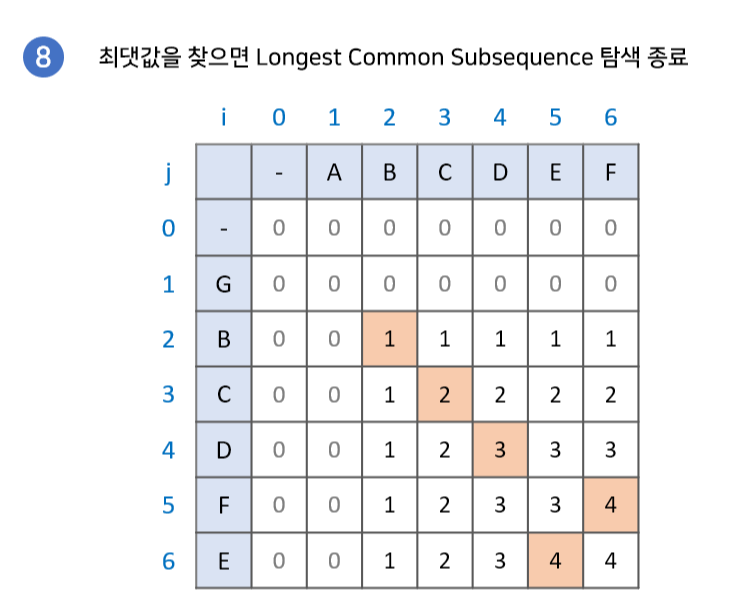
그럼 Longest Common Subsequence 구현과정을 좀 더 자세히 알아보면서 최장 공통 부분수열의 값을 찾아보자.
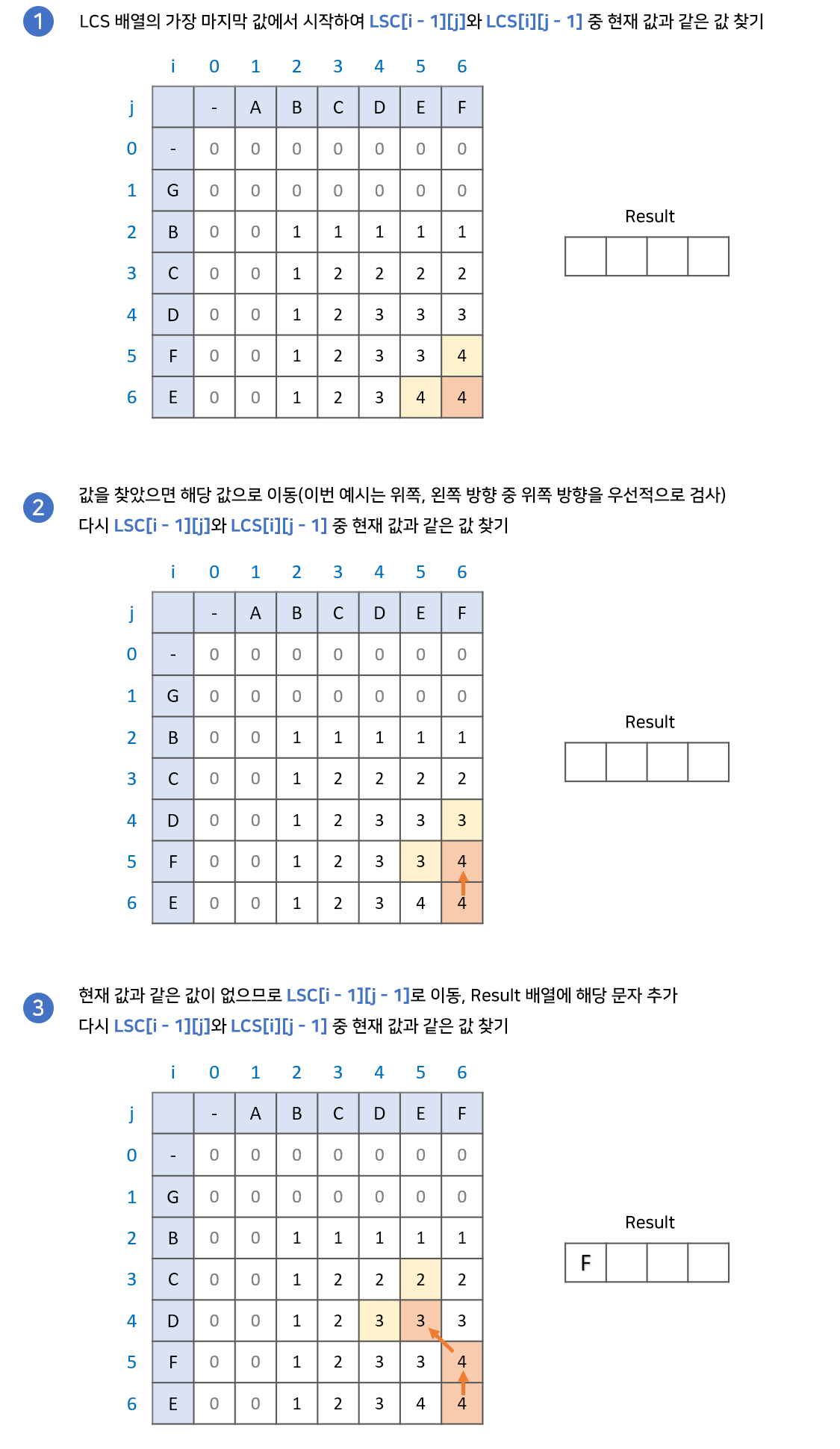
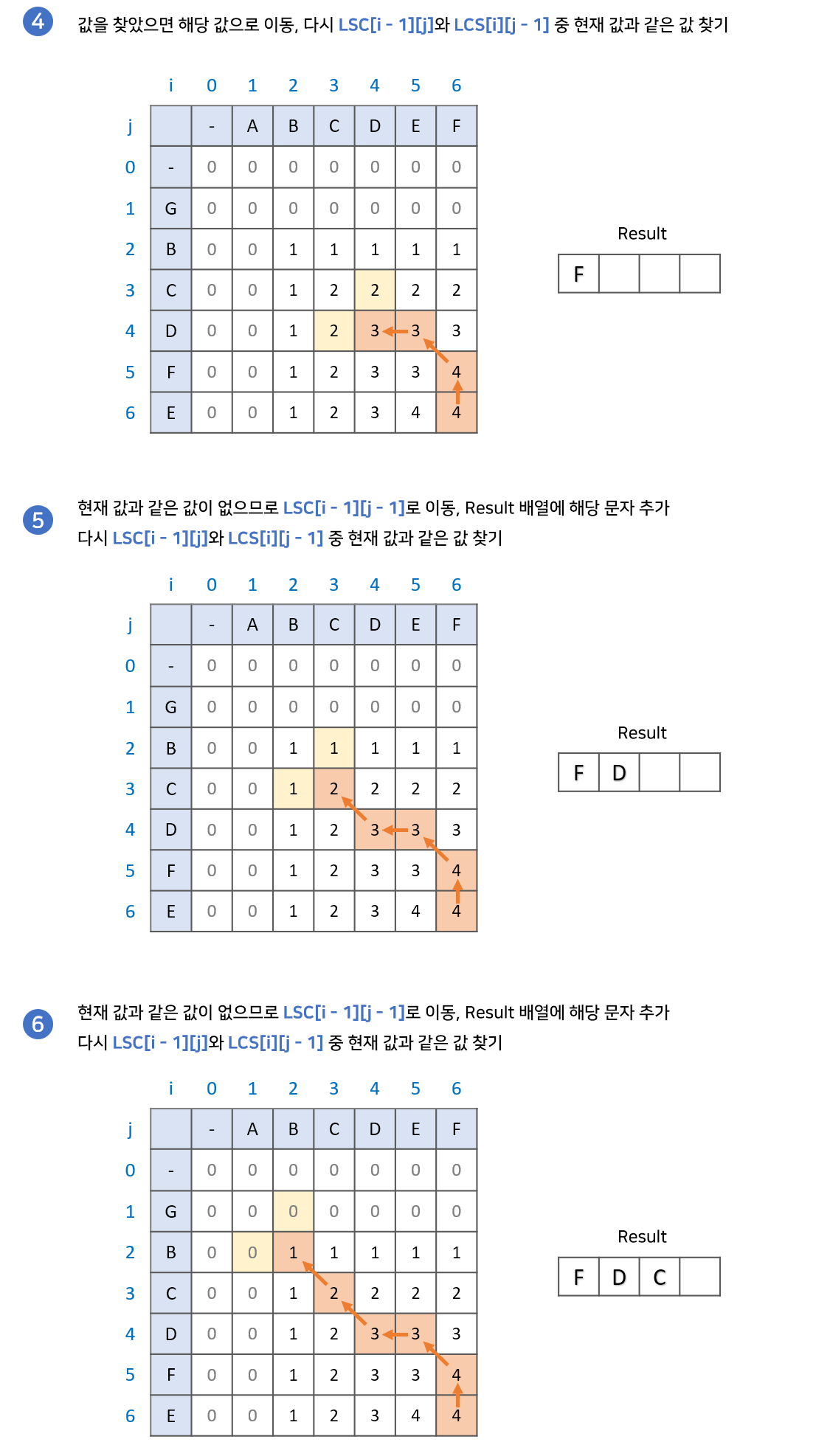
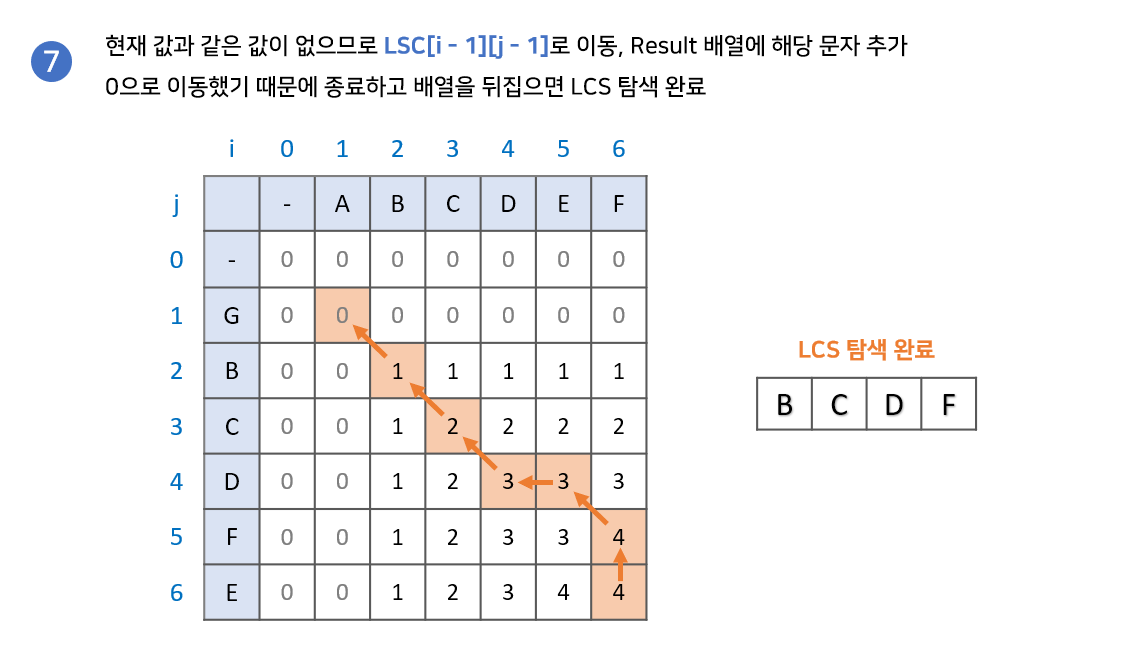
- LCS 배열의 가장 마지막 값에서 시작한다. 이때 결과값을 저장할 result 배열을 준비한다.
- LCS[i - 1][j]와 LCS[i][j - 1] 중 현재 값과 같은 값을 찾는다.
- 만약 같은 값이 있다면 해당 값으로 이동한다.
- 만약 같은 값이 없다면 result 배열에 해당 문자를 넣고 LCS[i - 1][j - 1]로 이동한다.
- 2번 과정을 반복하다 0으로 이동하게 되면 종료한다. 이때, result 배열의 역순이 LCS이다.
이와 관련된 LCS 백준 문제를 첨부한다.
KnapSack Problem
knapsack은 한국어로 배낭이다. 즉, 배낭 문제 혹은 배낭 알고리즘이고, 대표적인 DP 알고리즘이다. 그리고 이 것을 이번 단락에서 배운다고 생각하면 된다.
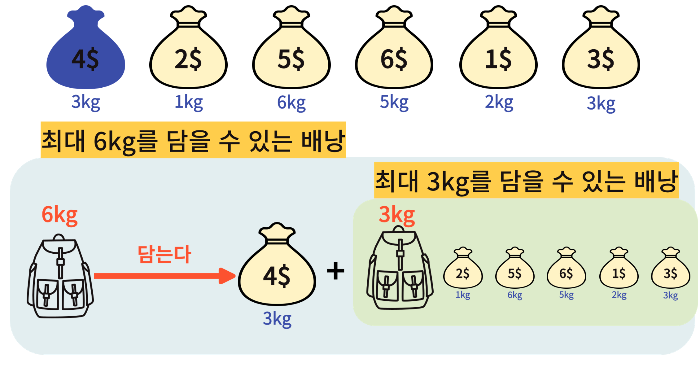
배낭 문제는 n개의 물건과 배낭이 있을 때, 각 물건에 가치와 무게가 존재한다. 또한 각 물건은 1개씩만 있으며, 배낭에는 담을 수 있는 최대 용량이 존재한다. 이러한 조건일 때, 배낭의 최대 용량을 초과하지 않으면서 배낭에 담을 수 있는 최대 가치의 합을 찾는 문제이다.
여기서 배낭 문제는 물건을 쪼갤 수 있는 Fraction Knapsack Problem과 물건을 쪼갤 수 없는 0-1 Knapsack Problem으로 나뉘는데, 일단 여기서는 0-1 Knapsack Problem을 설명한다.
우선 배낭 알고리즘이 Dynamic Programming인 이유는 결국 해당 물건을 배낭에 넣을 수 있는가 없는가에 대한 문제이기 때문이다. 따라서 크게보면 넣는다, 안 넣는다 2가지 선택지밖에 없다는 것이다.
이를 조금 더 알고리즘 적으로 해석해보면 다음과 같이 해석할 수 있을 것이다. 만약 최대 M까지 담을 수 있는 배낭이 있고 물건이 있을 때, 선택할 수 있는 경우의 수는 경우의 수는 결국 담기 or 안담기 2개이다. 그러면 상태는 가방에 공간이 (M-N) kg 남거나 그대로 M kg 남거나 둘 중 하나일 것이다. 그리고 단순히 이 과정을 가방에 더이상 공간이 없을 때까지 모든 물건에 대해 반복하는 것이다.
그럼 한번 이렇게 생각해보자. 최대 M을 담을 수 있는 배낭에 무게가 N이고 가치가 K인 물건을 담으면, 무게 N인 물건을 제외하고 최대 M-N kg을 담을 수 있는 배낭이 있는 것이다. 그러면 이 M-N kg인 배낭과 남은 물건들로 구성된 새로운 문제를 만드는 것이다. 즉, DP의 특징대로 부분의 답이 큰 부분의 답이 되고, 이 부분들의 답이 전체의 답이 되는 것이다.
정리하면 Knapsack Problem 에서 로직을 반복할 때 변하는 것은 딱 2가지이다.
- 배낭의 최대 무게
- 담을 수 있는 봉투의 개수 및 종류
이때, 경우의 수가 여러 가지로 갈리기 때문에 2차원 배열을 사용하여 각 경우의 수에 따른 답을 따로 저장해줘야 한다.
그러면 식을 다음과 같이 구성할 수 있다.
최대 이익[i][w] = 최대 무게가 w인 가방에서 i번째 물건까지 판단했을 때의 최대 가치
즉, 최대이익[i][w]의 의미는 최대 무게 6kg인 배낭에서 4번째 물건까지 진행했을 때의 최대 가치를 의미한다.
그럼 이 개념을 이용해 일반화를 진행해보자.

최대이익[i][w]는 어떤 값을 가질 것이고, 이를 편의상 dp[i][w]라고 부르자. 그럼 여기서 K + 1번째 물건을 탐색할 때의 최대 가치를 구해보는데, 다음과 같은 경우의 수로 나눌 수 있겠다.
- K + 1번째 물건의 무게가 최대 배낭 무게(W)를 초과하면, 최대 가치는 이전의 최대 가치인 K번째로 유지된다. 따라서 dp[K + 1][W] = dp[K][W] 이다.
- K + 1번째 물건의 무게가 최대 배낭 무게(W)를 초과하지 않으면, 2가지 경우의 수로 분리된다.
- K + 1번째 물건을 넣지 않는다. 그러면 dp[K+1][W] = dp[K][W]가 된다.
- K + 1번째 물건을 넣는다. 즉, 배낭 안에 해당 물건을 넣을 충분한 무게가 존재한다는 소리이다. 그런데 만약 배낭에 충분한 공간이 없다면 어떻게 해야할까? 안에 있는 물건을 빼고 해당 물건을 넣어야 한다. 즉, 최대 W kg까지 담을 수 있는 배낭이 K+1번째 물건을 담았을 때가 최대 가치라면 dp[K + 1][W] = (K + 1의 가치) + dp[K][W - M] 으로 일반항을 구할 수 있을 것이다.
정리하면, Knapsack Problem에 대한 경우에 따른 점화식을 구하면 다음과 같을 것이다.
- 만약, 물건 K의 무게 > 배낭 W의 무게
- dp[K][W] = dp[K - 1][W]
- 만약, 물건 K의 무게 <= 배낭 W의 무게
- dp[K][W] = max(dp[K - 1][W], K의 가치 + dp[K - 1][W - K 무게])
이렇게 점화식을 도출하면 이 개념을 가지고 재귀함수로 알고리즘을 구성해도 되고, 다른 방식으로 구성해도 된다.
이와 관련된 Knapsack 백준 문제를 첨부한다.
그리디 알고리즘
최적화 문제를 위한 알고리즘들은 통상적으로 일련의 단계를 거치는데, 각 단계마다 여러 가지 경우중에서 선택을 해야한다. 최적화 문제에서 동적 프로그래밍을 사용하면 가장 좋은 선택을 해야 한다. 그런데 이런 최적화 문제에서 동적 프로그래밍을 사용하면 가장 좋은 선택을 결정하기 위해서 지나치게 많은 일을 하게 된다. 오히려 더 간단하고 효율적인 알고리즘만으로도 충분한 경우가 많다. 그래서 이때 그리디 알고리즘을 사용하면 항상 각 단계에 있어서 가장 좋은 선택을 하게 된다. 다시 말해서 이 선택이 전체적으로 최적해로 안내하게 될 거라는 바람을 가지고 부분적으로 최적인 선택을 한다. 그래서 이번 단락에서는 그리디 알고리즘이 최적해를 제공할 수 있는 최적화 문제를 학습해보고자 한다.
그리디 알고리즘은 항상 최적의 해답을 구하지는 못하지만, 많은 문제에 대한 해를 구해줄 수는 있다. 예를 들어, activity-selection problem이라는 문제가 있는데, 이 문제를 먼저 동적 프로그래밍 방법으로 풀어보고 최적해에 도달하기 위해서 항상 그리디 선택을 해도 된다는 감을 잡기에 좋은 문제가 있다.
그리디 방법은 광범위한 문제에 적용이 된다. 그리디 방법의 응용에는 Minimum-spanning tree, 다익스트라 알고리즘 등이 알려져 있다.
그리디 방법의 요소들
그리디 알고리즘은 연속으로 선택하면서 문제의 최적해를 찾는다. 즉, 알고리즘에서 결정이 필요한 순간마다 가장 좋은 것으로 보이는 것을 선택한다. 물론 이런 방법은 항상 최적해를 찾지는 못하지만 activity-selection problem처럼 최적해를 찾는 경우도 있다.
그리고 일반적으로 다음 단계에 의해 그리디 알고리즘이 만들어진다.
- 하나의 선택을 하면 풀어야할 부분 문제도 하나만 남도록 최적화 문제를 바꾼다.
- 그리디 선택을 하는 것이 언제나 안전하도록 원래 문제의 최적해들 중에서 그리디 선택을 하는 것이 반드시 존재함을 증명한다.
- 그리디 선택을 했을 때, 그리디 선택과 남아있는 부분 문제에 대한 최적해와 결합하면 원래 문제에 대한 최적해를 얻음을 증명해 최적 부분 구조를 가진다는 것을 보인다.
그리고 기억해야할 점은 모든 그리디 알고리즘의 기저에는 더 많은 일을 해야하는 동적 프로그래밍 해가 거의 항상 존재한다는 것을 꼭 기억하자.
그리디 알고리즘의 2개의 중요 구성요소
그럼 또 필자의 입장에서는 동적 프로그래밍 때와 마찬가지로 그리디 알고리즘이 특정 최적화 문제를 풀 수 있을지 판별하는 기준을 세우고 싶다. 물론 언제나 되는 방법은 없지만 그리디 선택 특성과 최적 부분 구조는 2개의 중요한 구성요소가 될 수 있다. 따라서 어떤 문제가 이 특성을 가진다고 말할 수 있다면 그리디 알고리즘을 제대로 개발하는 중일 것이라고 말할 수 있을 것이다.
그리디 선택 특성
전체적인 최적해는 부분적인 최적 선택을 함으로써 만들 수 있다. 즉, 어떤 선택을 할지 고려할 때 부분 문제들의 결과를 고려할 필요없이 현재 고려중인 문제에서 최적으로 보이는 선택을 하면 된다. 이 점에서 그리디 알고리즘과 동적 프로그래밍이 다르다. 즉, 동적 프로그래밍에서는 단계마다 선택을 하고, 이 선택은 부분 문제의 해에 의존하게 된다. 결과적으로 동적 프로그래밍 문제는 일반적으로 상향식 접근으로 더 작은 부분 문제에서 더 큰 문제로 풀어나가는 방법으로 풀었다. 반면에 그리디 알고리즘에서는 현재 가장 좋아보이는 선택을 한 후에 그에 따라 생기는 부분 문제를 푼다. 따라서 그리디 알고리즘에 의해 선택을 하는 것은 지금까지 선택한 것에 의존하지만 미래의 선택이나 부분 문제의 해에는 의존할 수 없다. 정리하면, 동적 프로그래밍 알고리즘은 상향식 방법으로 진행하지만, 그리디 방법은 언제나 주어진 문제를 더 작은 문제로 만드는 그리디 선택을 계속하는 하향식 접근 방법으로 진행한다. 물론 매 단계마다 그리디 선택은 전역적으로 최적인 해를 만들어 낸다는 점을 증명해야 한다.
최적 부분 구조(optimal substructure)
어떤 문제에 대한 최적해가 그 문제의 부분 문제에 대한 최적래를 포함하고 있을 때, 그 문제를 최적 부분 구조를 가지고 있다고 말한다.
그리디와 동적 프로그래밍의 차이
동적 계획법과 탐욕법 모두 최적해를 구하는 문제에 사용되는 알고리즘이다. 동적 계획법은 작은 문제의 최적해가 전체 문제의 최적해가 되므로 현재 구하는 답이 최적해인 게 보장된다. 반면 탐욕법은 한 수 앞만 보고 진행을 하기 때문에 항상 최적해를 보장하지는 않는다. 정리해보면 동적 계획법은 속도 측면에서는 탐욕법보다 느리지만 확실한 답이 보장되고, 탐욕법은 동적 계획법보다 속도는 빠른 대신 확실한 답이 보장되지 않는다. 그러므로 문제를 풀 때 탐욕법으로 풀릴만한 문제인지 아닌지를 잘 판단하고 적당한 풀이 과정을 세우는 것이 시간을 단축시키는 방법이 될 것이다.
인용
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.
velog.io
https://howudong.tistory.com/106
배낭 문제(KnapSack Problem) 그림으로 쉽게 이해하기
배낭 알고리즘이란? 배낭 문제(Knapsack)는 n개의 물건과 배낭 있을 때, 각 물건에는 가치와 무게가 존재한다. 또한 각 물건은 1개씩만 있다. 배낭에는 담을 수 있는 최대 용량이 존재한다. 이러한
howudong.tistory.com
https://jaejade.tistory.com/40
동적 계획법 알고리즘 (Dynamic programming Algorithm)
동적 계획법 알고리즘이란 동적 계획법이란 하나의 복잡한 문제를 여러 개의 간단한 하위 문제로 나누어 푼 다음, 이를 결합하여 답을 도출해내는 방법이다. 나누어진 하위 문제들의 결과를 따
jaejade.tistory.com
'컴퓨터 사이언스 > Algorithm' 카테고리의 다른 글
| 힙 정렬 (0) | 2023.11.13 |
|---|---|
| Dynamic Programming (0) | 2023.10.26 |
| 분리 집합(Disjoint Set): Union-Find (1) | 2023.10.21 |
| 최소 스패닝 트리(MST. Minimum Spanning Tree) (0) | 2023.10.21 |
| 최단 거리 알고리즘 정리 (1) | 2023.10.20 |
