heap sort는 힙의 특성을 이용하여 정렬하는 알고리즘이다. 여기서 힙은 부모의 값이 자식의 값보다 항상 크다는 조건을 만족하는 완전 이진 트리이다. 이때 부모의 값이 자식의 값보다 항상 작아도 힙이라고 한다. 즉, 이러한 두 값의 대소 관계가 일정하면 된다.
따라서 힙에서 어떤 부모와 자식 관계를 주목할 때, 부모의 값이 자식의 값보다 항상 큰 관계가 성립한다. 따라서 힙의 가장 위쪽에 위치한 루트가 가장 큰 값이 된다. 다만, 힙에서 부모와 자식 관계는 일정하지만, 형제 사이의 대소 관계는 일정하지 않다. 따라서 힙은 형제의 대소 관계가 정해져 있지 않으므로, 부분 순서 트리(partial ordered tree)라고도 한다.
그럼 이번에는 힙의 원소를 배열에 어떻게 저장할 것인지를 알아보자. 먼저 가장 위쪽에 있는 루트를 배열의 첫 번째 인덱스에 저장한다. 그리고 한 단계 아래에서 왼쪽 원소에서 오른쪽 원소로 따라간다. 이 과정에서 배열의 인덱스 값을 1씩 증가시키면서 각 원소를 저장한다. 이 작업을 가장 마지막에 있는 원소까지 반복하여 힙을 배열에 저장하면 완료된다.

이러한 순서로 힙을 배열에 저장하면 부모 인덱스와 왼쪽 자식, 오른쪽 자식 인덱스 사이에는 다음과 같은 관계가 성립한다.
원소 a[i]에서
부모 : a[(i - 1) // 2]
왼쪽 자식 : a[i * 2 + 1]
오른쪽 자식 : a[i * 2 + 2]
그럼 이제 힙 정렬의 특징에 대해서 정리해보자.
힙 정렬이란 '힙에서 최댓값은 루트에 위치한다'는 특징을 이용하여 정렬하는 알고리즘이고, 구체적으로 다음과 같은 작업을 반복한다.
- 힙에서 최댓값인 루트를 꺼낸다.
- 루트 이외의 부분을 힙으로 만든다.
그리고 이 과정에서 꺼낸 값을 나열하면 정렬이 끝난 배열이 완성된다. 즉, 힙 정렬은 선택 정렬을 응용한 알고리즘인 것이다.
또한 힙 정렬에서 최댓값인 루트를 꺼낸 뒤, 다시 남은 원소 중에서 최댓값을 구해야 한다. 즉, 루트를 꺼내고 남은 원소로 구성한 트리도 힙이 되도록 재구성해야 한다는 뜻이다.
루트를 삭제한 힙의 재구성
루트를 삭제하고, 힙을 다시 구성하는 순서는 다음과 같다.
- 루트를 삭제하고, 마지막 원소(가장 하단의 오른쪽에 위치한 원소)를 루트로 이동한다.
- 루트에서 시작하여 자신보다 값이 큰 자식과 자리를 바꾸고, 아래쪽으로 내려가는 작업을 반복한다.
- 자식의 값이 작거나 리프의 위치에 도달하면 종료한다.
힙 정렬 알고리즘 알아보기
힙 정렬 과정을 단순화해서 나타내면 다음과 같다. 단, 여기서 n값은 배열의 원소 수이고, i값은 배열의 마지막 인덱스이다. 그리고 배열의 맨 끝에 최대값부터 순서대로 하나씩 저장된다는 사실을 인식하자.
- i 값을 n - 1로 초기화한다.
- a[0] 루트값과 정렬이 완료된 배열의 값을 나타내는 a[i] 값을 교환한다.
- a[0], a[1], a[2] .. a[i - 1]을 힙으로 만든다.
- i값을 1씩 감소시켜서 0이 되면 종료한다. 그렇지 않으면 2번으로 돌아간다.
이 순서대로 힙 정렬을 수행하는데, 이때 중요한 것이 배열의 처음 상태가 힙의 요구사항을 만족하지 않을 수도 있다는 것이다. 따라서 이 순서를 적용하기 전에 배열을 반드시 힙으로 만들어야 한다.
배열을 힙으로 만들기
배열을 힙으로 만드는 과정은 가장 아랫부분의 작은 서브트리부터 상향식으로 진행하여 전체 배열을 힙으로 만드는 것이다. 먼저 가장 아랫부분의 오른쪽 서브트리의 힙을 만들고, 같은 단계에 있는 왼쪽 서브트리로 진행한다. 그 단계를 완료하면 한 단계 위로 이동하면서 각각의 서브트리를 힙으로 만든다.
직접 손으로 힙 정렬 수행해보기
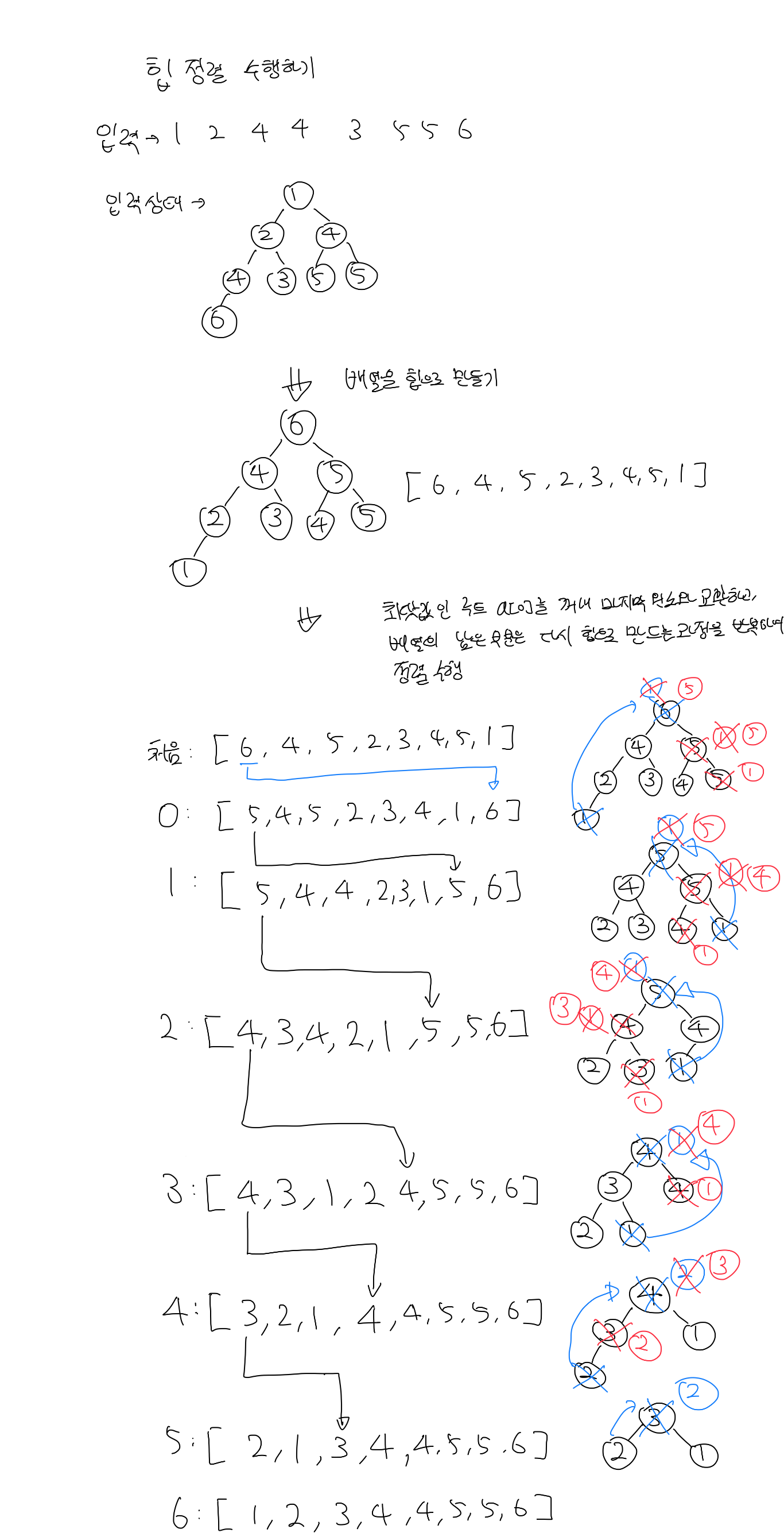
백준 2750
힙 정렬은 시간 복잡도가 O(n logn)이기 때문에 선택 정렬의 O(n^2)보다 훨씬 빠르고, 백준 2750번 문제를 내장 sorted 함수로 풀었을 때보다 더 빠른 시간 복잡도를 가질 수 있었다.
import sys
input = lambda: sys.stdin.readline().rstrip()
N = int(input())
heap = [int(input()) for _ in range(N)]
def down_heap(arr, left, right):
root = arr[left]
parent = left
while parent < (right + 1) // 2:
child_left = parent * 2 + 1
child_right = child_left + 1
child = child_right if child_right <= right and arr[child_right] > arr[child_left] else child_left
if root >= arr[child]:
break
arr[parent] = arr[child]
parent = child
arr[parent] = root
for i in range((N - 1) // 2, -1, -1):
down_heap(heap, i, N - 1)
for i in range(N - 1, 0, -1):
heap[0], heap[i] = heap[i], heap[0],
down_heap(heap, 0, i - 1)
for value in heap:
print(value)'컴퓨터 사이언스 > Algorithm' 카테고리의 다른 글
| 동적 프로그래밍과 그리디 알고리즘 (0) | 2023.10.27 |
|---|---|
| Dynamic Programming (0) | 2023.10.26 |
| 분리 집합(Disjoint Set): Union-Find (1) | 2023.10.21 |
| 최소 스패닝 트리(MST. Minimum Spanning Tree) (0) | 2023.10.21 |
| 최단 거리 알고리즘 정리 (1) | 2023.10.20 |
